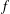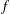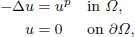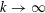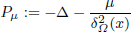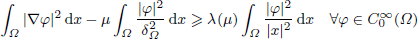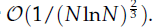Refine listing
Actions for selected content:
102 results in 35Pxx
THE STEKLOV SPECTRUM OF CUBOIDS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 06 December 2018, pp. 272-310
- Print publication:
- 2019
-
- Article
- Export citation
ASYMPTOTIC BEHAVIOUR OF THE SPECTRA OF SYSTEMS OF MAXWELL EQUATIONS IN PERIODIC COMPOSITE MEDIA WITH HIGH CONTRAST
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 23 April 2018, pp. 583-605
- Print publication:
- 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REDUCTION OF DIMENSION AS A CONSEQUENCE OF NORM-RESOLVENT CONVERGENCE AND APPLICATIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 406-429
- Print publication:
- 2018
-
- Article
- Export citation
Fractional eigenvalue problems that approximate Steklov eigenvalue problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 December 2017, pp. 499-516
- Print publication:
- June 2018
-
- Article
- Export citation
Normalized solutions for nonlinear Schrödinger systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 20 November 2017, pp. 225-242
- Print publication:
- April 2018
-
- Article
- Export citation
BOUND STATES IN WEAKLY DEFORMED WAVEGUIDES: NUMERICAL VERSUS ANALYTICAL RESULTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 03 October 2017, pp. 200-214
-
- Article
-
- You have access
- Export citation
Quasi boundary triples and semi-bounded self-adjoint extensions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 28 June 2017, pp. 895-916
- Print publication:
- October 2017
-
- Article
- Export citation
Small eigenvalues of surfaces of finite type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 8 / August 2017
- Published online by Cambridge University Press:
- 05 June 2017, pp. 1747-1768
- Print publication:
- August 2017
-
- Article
- Export citation
On isotropic cloaking and interior transmission eigenvalue problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 22 May 2017, pp. 253-280
-
- Article
- Export citation
ON THE EXISTENCE OF
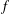 $f$ -MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
$f$ -MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 317-325
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
A Comparison of Fourier Spectral Iterative Perturbation Method and Finite Element Method in Solving Phase-Field Equilibrium Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 27 March 2017, pp. 1325-1349
- Print publication:
- May 2017
-
- Article
- Export citation
NONCLASSICAL SPECTRAL ASYMPTOTICS AND DIXMIER TRACES: FROM CIRCLES TO CONTACT MANIFOLDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 23 January 2017, e3
-
- Article
-
- You have access
- Open access
- Export citation
A short remark regarding Pohozaev-type results on general domains assuming finite Morse index
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 293-297
- Print publication:
- April 2017
-
- Article
- Export citation
Neumann to Steklov eigenvalues: asymptotic and monotonicity results
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 429-447
- Print publication:
- April 2017
-
- Article
- Export citation
MINIMIZING DIRICHLET EIGENVALUES ON CUBOIDS OF UNIT MEASURE
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 469-482
- Print publication:
- 2017
-
- Article
- Export citation
Homogenization and norm-resolvent convergence for elliptic operators in a strip perforated along a curve
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 08 November 2016, pp. 1115-1158
- Print publication:
- December 2016
-
- Article
- Export citation
Optimal Hardy inequalities in cones
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2016, pp. 89-124
- Print publication:
- February 2017
-
- Article
- Export citation
Pseudo-Arclength Continuation Algorithms for Binary Rydberg-Dressed Bose-Einstein Condensates
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 1067-1093
- Print publication:
- April 2016
-
- Article
- Export citation
ON THE FIRST EIGENCONE FOR THE FINSLER LAPLACIAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 316-325
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
An Adaptive Finite Element Method with Hybrid Basis for Singularly Perturbed Nonlinear Eigenvalue Problems
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 442-472
- Print publication:
- February 2016
-
- Article
- Export citation
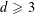
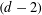
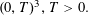
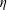
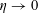
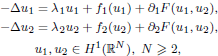
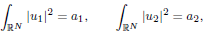
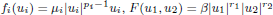 , with positive constants
, with positive constants 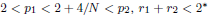 in dimensions 2 ≤
in dimensions 2 ≤