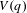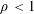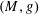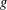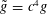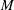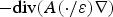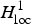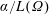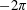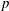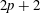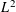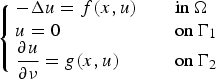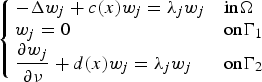Refine listing
Actions for selected content:
102 results in 35Pxx
GLOBAL SUBELLIPTIC ESTIMATES FOR KRAMERS–FOKKER–PLANCK OPERATORS WITH SOME CLASS OF POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 22 June 2020, pp. 675-711
- Print publication:
- March 2022
-
- Article
- Export citation
Estimates for sums and gaps of eigenvalues of Laplacians on measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 842-861
- Print publication:
- April 2021
-
- Article
- Export citation
The spectrum of the mean curvature operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 01 April 2020, pp. 451-463
- Print publication:
- April 2021
-
- Article
- Export citation
ON NONUNIQUENESS FOR THE ANISOTROPIC CALDERÓN PROBLEM WITH PARTIAL DATA
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 January 2020, e7
-
- Article
-
- You have access
- Open access
- Export citation
Generalizations of Menchov–Rademacher Theorem and Existence of Wave Operators in Schrödinger Evolution
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 20 December 2019, pp. 360-382
- Print publication:
- April 2021
-
- Article
- Export citation
Generalized eigenvalues of the (P, 2)-Laplacian under a parametric boundary condition
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 287-303
-
- Article
- Export citation
Hypersurfaces with Prescribed Boundary and Small Steklov Eigenvalues
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 46-57
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Green Function and Self-adjoint Laplacians on Polyhedral Surfaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 02 July 2019, pp. 1324-1351
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
First-order expansions for eigenvalues and eigenfunctions in periodic homogenization
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 20 March 2019, pp. 2189-2215
- Print publication:
- October 2020
-
- Article
- Export citation
From Steklov to Neumann and Beyond, via Robin: The Szegő Way
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 07 March 2019, pp. 1024-1043
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Eigenvalue Optimisation on Flat Tori and Lattice Points in Anisotropically Expanding Domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 07 March 2019, pp. 967-987
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Spectral transitions for Aharonov-Bohm Laplacians on conical layers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1663-1687
- Print publication:
- December 2019
-
- Article
- Export citation
Bifurcation of nonlinear bound states in the periodic Gross-Pitaevskii equation with 𝒫𝒯-symmetry
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 171-204
- Print publication:
- February 2020
-
- Article
- Export citation
Some generic properties of Schrödinger operators with radial potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1435-1451
- Print publication:
- December 2019
-
- Article
- Export citation
Asymptotic approximations for the plasmon resonances of nearly touching spheres
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 246-276
-
- Article
- Export citation
The Steklov Problem on Differential Forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 417-435
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
CENTRAL LIMIT THEOREM FOR PLANCK-SCALE MASS DISTRIBUTION OF TORAL LAPLACE EIGENFUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 643-676
- Print publication:
- 2019
-
- Article
- Export citation
Bifurcation and standing wave solutions for a quasilinear Schrödinger equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 939-968
- Print publication:
- August 2019
-
- Article
- Export citation
Morse index and symmetry for elliptic problems with nonlinear mixed boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 305-324
- Print publication:
- April 2019
-
- Article
- Export citation
Nonlocal problems arising from the birth-jump processes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 447-469
- Print publication:
- April 2019
-
- Article
- Export citation