Refine listing
Actions for selected content:
102 results in 35Pxx
SPECTRAL THEORETIC CHARACTERIZATION OF THE MASSLESS DIRAC ACTION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 08 March 2016, pp. 701-718
- Print publication:
- 2016
-
- Article
-
- You have access
- Open access
- Export citation
EIGENVALUE HOMOGENISATION PROBLEM WITH INDEFINITE WEIGHTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 15 October 2015, pp. 113-127
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Scattering of Herglotz waves from periodic structures and mapping properties of the Bloch transform
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 08 October 2015, pp. 1283-1311
- Print publication:
- December 2015
-
- Article
- Export citation
Error Estimates of Some Numerical Atomic Orbitals in Molecular Simulations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 125-146
- Print publication:
- July 2015
-
- Article
- Export citation
ON THE RESOLVENT OF THE LAPLACE–BELTRAMI OPERATOR IN HYPERBOLIC SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 24 April 2015, pp. 186-206
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
EXPANSION CONSTANTS AND HYPERBOLIC EMBEDDINGS OF FINITE GRAPHS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 19 November 2014, pp. 1-13
- Print publication:
- January 2015
-
- Article
- Export citation
Spectre et géométrie conforme des variétés compactes à bord
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 28 October 2014, pp. 2112-2126
- Print publication:
- December 2014
-
- Article
- Export citation
Compactness of embeddings of function spaces on quasi-bounded domains and the distribution of eigenvalues of related elliptic operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 829-851
-
- Article
-
- You have access
- Export citation
Spectral and dynamical properties of sparse one-dimensional continuous Schrödinger and Dirac operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 667-700
-
- Article
-
- You have access
- Export citation
Improved local energy decay for the wave equation on asymptotically Euclidean odd dimensional manifolds in the short range case
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 13 July 2012, pp. 635-650
- Print publication:
- July 2013
-
- Article
- Export citation
The L2 restriction norm of a GL3 Maass form
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 20 March 2012, pp. 675-717
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Tunnel effect and symmetries for Kramers–Fokker–Planck type operators
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 12 May 2011, pp. 567-634
- Print publication:
- July 2011
-
- Article
- Export citation
CONTINUITY OF THE VARIATIONAL EIGENVALUES OF THE p-LAPLACIAN WITH RESPECT TO p
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 15 March 2011, pp. 376-381
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Solvability conditions for some non-Fredholm operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 30 November 2010, pp. 249-271
-
- Article
-
- You have access
- Export citation
ON THE ISOPERIMETRIC PROBLEM FOR THE LAPLACIAN WITH ROBIN AND WENTZELL BOUNDARY CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 348-350
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Spectral Convergence for High-Contrast Elliptic Periodic Problems with a Defect Via Homogenization
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 29-57
- Print publication:
- December 2009
-
- Article
- Export citation
Trapped modes in a waveguide with a thick obstacle
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 171-186
- Print publication:
- December 2004
-
- Article
- Export citation
Strong ergodicity for Markov processes by coupling methods
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 839-852
- Print publication:
- December 2002
-
- Article
- Export citation
An extension of the principle of spatial averaging for inertial manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-142
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
The difference of consecutive eigenvalues
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-315
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
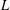
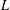
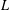

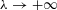
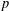
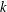
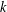
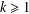

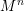
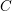
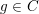
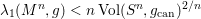
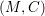
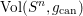
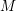
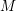
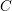
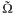 (the
(the 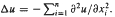 . We prove an inequality involving the first
. We prove an inequality involving the first