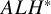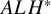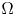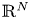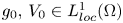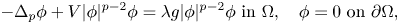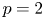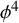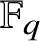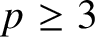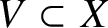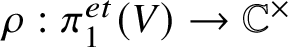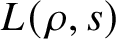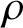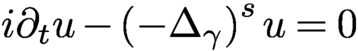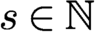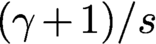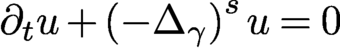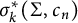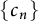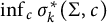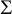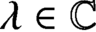Refine listing
Actions for selected content:
103 results in 35Pxx
Optimization of the anisotropic Cheeger constant with respect to the anisotropy
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 1030-1043
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE LOWEST EIGENVALUE OF THE FRACTIONAL LAPLACIAN FOR THE INTERSECTION OF TWO DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 02 December 2022, pp. 290-297
- Print publication:
- October 2023
-
- Article
- Export citation
The Torelli theorem for
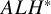 $ALH^*$ gravitational instantons
$ALH^*$ gravitational instantons
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 September 2022, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the optimization of the first weighted eigenvalue
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 1777-1804
- Print publication:
- December 2023
-
- Article
- Export citation
Quadratic Klein-Gordon equations with a potential in one dimension
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 11 July 2022, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
p-Adic estimates of abelian Artin L-functions on curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 January 2022, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotics of sloshing eigenvalues for a triangular prism
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 20 December 2021, pp. 539-571
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Index estimates for closed minimal submanifolds of the sphere
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 December 2021, pp. 802-816
- Print publication:
- June 2022
-
- Article
- Export citation
Equitable colourings of Borel graphs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 November 2021, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SMALL-SCALE EQUIDISTRIBUTION OF RANDOM WAVES GENERATED BY AN UNFAIR COIN FLIP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 29 November 2021, pp. 222-252
-
- Article
- Export citation
OBSERVABILITY OF BAOUENDI–GRUSHIN-TYPE EQUATIONS THROUGH RESOLVENT ESTIMATES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 14 June 2021, pp. 541-579
- Print publication:
- March 2023
-
- Article
- Export citation
Asymptotics of the principal eigenvalue of the Laplacian in 2D periodic domains with small traps
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 04 June 2021, pp. 646-673
-
- Article
- Export citation
Bihomogeneous symmetric functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 25 May 2021, pp. 400-408
- Print publication:
- June 2022
-
- Article
- Export citation
Degenerating sequences of conformal classes and the conformal Steklov spectrum
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 05 March 2021, pp. 1093-1136
- Print publication:
- August 2022
-
- Article
- Export citation
On the first eigenvalue of the Laplace operator for compact spacelike submanifolds in Lorentz–Minkowski spacetime 𝕃m
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 311-330
- Print publication:
- April 2022
-
- Article
- Export citation
Strichartz estimates for orthonormal families of initial data and weighted oscillatory integral estimates
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e1
-
- Article
-
- You have access
- Open access
- Export citation
Almost all Steiner triple systems are almost resolvable
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 03 November 2020, e39
-
- Article
-
- You have access
- Open access
- Export citation
Continuity of solutions for the Δϕ-Laplacian operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 1355-1382
- Print publication:
- August 2021
-
- Article
- Export citation
On the policy improvement algorithm for ergodic risk-sensitive control
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 1305-1330
- Print publication:
- August 2021
-
- Article
- Export citation
Bounded solutions for an ordinary differential system from the Ginzburg–Landau theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 14 August 2020, pp. 3378-3408
- Print publication:
- December 2020
-
- Article
- Export citation