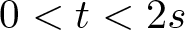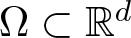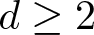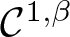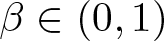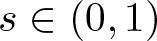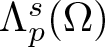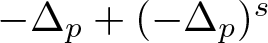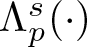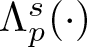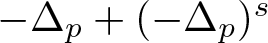Refine listing
Actions for selected content:
229 results in 35Rxx
Superlinear problems involving nonlinear superposition operators of mixed fractional order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 January 2026, pp. 1-26
-
- Article
- Export citation
Multipeak solutions for fractional elliptic equations on conformal infinities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 December 2025, pp. 1-55
-
- Article
- Export citation
Normalized solutions of L2-supercritical NLS equations on non-compact metric graphs
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 December 2025, pp. 1-34
-
- Article
- Export citation
Monotonicity of positive solutions to equations involving fractional p-Laplacian in coercive epigraph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-13
-
- Article
-
- You have access
- HTML
- Export citation
On the Γ-limit of weighted fractional energies
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantitative stability in fractional Hardy–Sobolev inequalities: the role of Euler–Lagrange equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-39
-
- Article
- Export citation
Global well-posedness and soliton resolution for the half-wave maps equation with rational data
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 November 2025, e190
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a Cahn–Hilliard equation for the growth and division of chemically active droplets modelling protocells
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 November 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two uniqueness results in the inverse boundary value problem for the weighted p-Laplace equation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e147
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Blow-up of cylindrically symmetric solutions for fractional NLS
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On global fractional Calderón–Zygmund regularity for the fractional Dirichlet problem on Lipschitz domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-31
-
- Article
- Export citation
STABILITY RESULTS FOR NONLOCAL SERRIN-TYPE PROBLEMS, ANTISYMMETRIC HARNACK INEQUALITIES AND GEOMETRIC ESTIMATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 04 July 2025, pp. 394-396
- Print publication:
- October 2025
-
- Article
-
- You have access
- HTML
- Export citation
The evolution problem for the 1D nonlocal Fisher-KPP equation with a top hat kernel. Part 2. The initial-boundary value problem on a finite domain
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Correspondence between Pestov and Weitzenböck identities
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 02 May 2025, pp. 443-463
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal transport on gas networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Determination of period matrix of double of surface with boundary via its DN map
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-24
-
- Article
- Export citation
Hardy and Rellich Inequalities with Bessel Pairs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 825-842
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic Pre-Complexes, Hodge-like Decompositions and Overdetermined Boundary-Value Problems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 March 2025, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solution theory of fractional SDEs in complete subcritical regimes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strict Faber–Krahn-type inequality for the mixed local–nonlocal operator under polarization
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 506-525
-
- Article
- Export citation