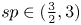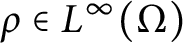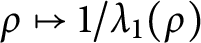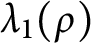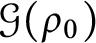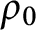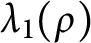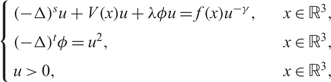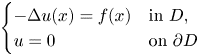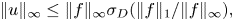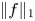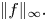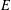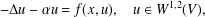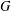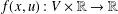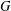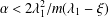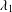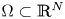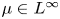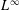Refine listing
Actions for selected content:
228 results in 35Rxx
Continuity of solutions for the Δϕ-Laplacian operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 1355-1382
- Print publication:
- August 2021
-
- Article
- Export citation
Continuous-domain assignment flows
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 01 September 2020, pp. 570-597
-
- Article
- Export citation
POINCARÉ AND SOBOLEV INEQUALITIES FOR DIFFERENTIAL FORMS IN HEISENBERG GROUPS AND CONTACT MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 29 June 2020, pp. 869-920
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Approximate solutions to one-phase Stefan-like problems with space-dependent latent heat
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 337-369
-
- Article
- Export citation
HALF-SPACE MACDONALD PROCESSES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e11
-
- Article
-
- You have access
- Open access
- Export citation
Local minimizers in absence of ground states for the critical NLS energy on metric graphs
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 22 May 2020, pp. 705-733
- Print publication:
- April 2021
-
- Article
- Export citation
SEMILINEAR CALDERÓN PROBLEM ON STEIN MANIFOLDS WITH KÄHLER METRIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 132-144
- Print publication:
- February 2021
-
- Article
- Export citation
Concentration of positive solutions for a class of fractional p-Kirchhoff type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 May 2020, pp. 601-651
- Print publication:
- April 2021
-
- Article
- Export citation
Extended Stefan problem for the solidification of binary alloys in a sphere
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 May 2020, pp. 242-279
-
- Article
- Export citation
Steiner symmetry in the minimization of the first eigenvalue of a fractional eigenvalue problem with indefinite weight
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 14 April 2020, pp. 970-992
- Print publication:
- August 2021
-
- Article
- Export citation
Existence and stability of bistable wavefronts in a nonlocal delayed reaction–diffusion epidemic system
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 March 2020, pp. 146-176
-
- Article
- Export citation
FRACTIONAL SCHRÖDINGER–POISSON SYSTEM WITH SINGULARITY: EXISTENCE, UNIQUENESS, AND ASYMPTOTIC BEHAVIOR
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 179-192
- Print publication:
- January 2021
-
- Article
-
- You have access
- Export citation
Optimal stopping for the exponential of a Brownian bridge
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 361-384
- Print publication:
- March 2020
-
- Article
- Export citation
On the L∞-maximization of the solution of Poisson's equation: Brezis–Gallouet–Wainger type inequalities and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 79-92
- Print publication:
- February 2021
-
- Article
- Export citation
ON A CLASS OF NONLINEAR SCHRÖDINGER EQUATIONS ON FINITE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 477-487
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Nonlinear fractional Laplacian problems with nonlocal ‘gradient terms’
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 04 February 2020, pp. 2682-2718
- Print publication:
- October 2020
-
- Article
- Export citation
HIGH ORDER PARACONTROLLED CALCULUS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 02 December 2019, e44
-
- Article
-
- You have access
- Open access
- Export citation
CALDERÓN’S INVERSE PROBLEM WITH A FINITE NUMBER OF MEASUREMENTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 08 October 2019, e35
-
- Article
-
- You have access
- Open access
- Export citation
Cauchy problem and periodic homogenization for nonlocal Hamilton–Jacobi equations with coercive gradient terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 17 September 2019, pp. 3028-3059
- Print publication:
- December 2020
-
- Article
- Export citation
Liouville theorem for fractional Hénon–Lane–Emden systems on a half space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 17 September 2019, pp. 3060-3073
- Print publication:
- December 2020
-
- Article
- Export citation