Refine listing
Actions for selected content:
219 results in 35Rxx
On the Disorder Problem for a Negative Binomial Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 167-179
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Generalized Morrey Regularity for Parabolic Equations with Discontinuous Data
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 10 December 2014, pp. 199-218
-
- Article
-
- You have access
- Export citation
The stochastic filtering problem: a brief historical account
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 13-22
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
SOBOLEV SPACES ON LOCALLY COMPACT ABELIAN GROUPS AND THE BOSONIC STRING EQUATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 39-53
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
EXISTENCE RESULTS FOR A CLASS OF ABSTRACT IMPULSIVE DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 18 March 2013, pp. 366-385
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
New global stability estimates for the Calderón problem in two dimensions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 07 June 2012, pp. 553-569
- Print publication:
- July 2013
-
- Article
- Export citation
Dimension reduction and homogenization of random degenerate operators. Part I
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 January 2012, pp. 1-22
-
- Article
-
- You have access
- Export citation
A topological index theorem for manifolds with corners
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 640-668
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Efficient nonlinear filtering of a singularly perturbed stochastic hybrid system
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 November 2011, pp. 254-270
-
- Article
-
- You have access
- Export citation
Optimal control of stochastic delay equations and time-advanced backward stochastic differential equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 572-596
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
COMPARISON OF NUMERICAL AND ANALYTICAL APPROXIMATIONS OF THE EARLY EXERCISE BOUNDARY OF AMERICAN PUT OPTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 4 / April 2010
- Published online by Cambridge University Press:
- 21 December 2010, pp. 430-448
-
- Article
-
- You have access
- Export citation
TRAVELLING WAVE SOLUTIONS IN NONLOCAL REACTION–DIFFUSION SYSTEMS WITH DELAYS AND APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 1 / July 2009
- Published online by Cambridge University Press:
- 09 March 2010, pp. 49-66
-
- Article
-
- You have access
- Export citation
Interior h1 Estimates for Parabolic Equations with LMO Coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 202-217
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
EXISTENCE RESULTS FOR ABSTRACT DEGENERATE NEUTRAL FUNCTIONAL DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 13 January 2010, pp. 329-342
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Generalized oscillatory integrals and Fourier integral operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 351-386
-
- Article
-
- You have access
- Export citation
EXISTENCE OF S-ASYMPTOTICALLY ω-PERIODIC SOLUTIONS FOR ABSTRACT NEUTRAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 365-382
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Hitting Time and Inverse Problems for Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 640-649
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Nonsmooth critical point theory and nonlinear elliptic equations at resonance
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 245-271
- Print publication:
- October 2000
-
- Article
-
- You have access
- Export citation
A free surface problem arising in the drainage of a uniformly irrigated field: Existence and uniqueness results
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 389-403
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
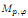 of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global
of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global 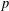
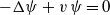
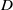

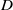
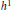
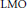
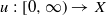 is said to be
is said to be 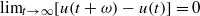 . This paper is devoted to study the existence and qualitative properties of
. This paper is devoted to study the existence and qualitative properties of 