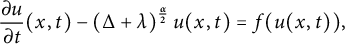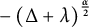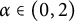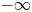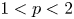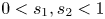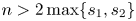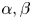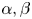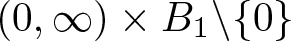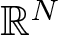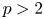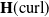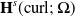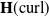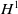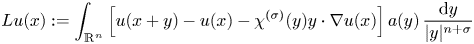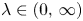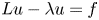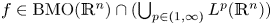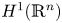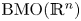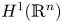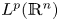Refine listing
Actions for selected content:
228 results in 35Rxx
Characterising small objects in the regime between the eddy current model and wave propagation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 08 August 2023, pp. 294-317
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The effect of pore-scale contaminant distribution on the reactive decontamination of porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 08 August 2023, pp. 318-358
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the joint survival probability of two collaborating firms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 August 2023, pp. 369-384
- Print publication:
- June 2024
-
- Article
- Export citation
Sliding methods for tempered fractional parabolic problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1358-1378
- Print publication:
- August 2024
-
- Article
- Export citation
On large solutions for fractional Hamilton–Jacobi equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 1313-1335
- Print publication:
- October 2024
-
- Article
- Export citation
OPTIMAL STOPPING PROBLEMS WITH A RANDOM TIME HORIZON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 345-346
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Homogenization of non-symmetric jump processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 1-33
- Print publication:
- March 2024
-
- Article
- Export citation
On a class of nonlocal continuity equations on graphs
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 17 May 2023, pp. 109-126
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonexistence of anti-symmetric solutions for fractional Hardy–Hénon system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 15 May 2023, pp. 862-886
- Print publication:
- June 2024
-
- Article
- Export citation
Spreading dynamics of a discrete Nicholson's blowflies equation with distributed delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 746-768
- Print publication:
- June 2024
-
- Article
- Export citation
Higher-order evolution inequalities involving convection and Hardy-Leray potential terms in a bounded domain
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 05 May 2023, pp. 366-390
-
- Article
- Export citation
Increasing stability for the inverse source problem in elastic waves with attenuation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 896-910
-
- Article
- Export citation
Convergence for the fractional p-Laplacian and its application to the extended Nirenberg problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 05 April 2023, pp. 660-672
- Print publication:
- April 2024
-
- Article
- Export citation
The monostable cooperative system with nonlocal diffusion and free boundaries
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 629-659
- Print publication:
- April 2024
-
- Article
- Export citation
Extending linear growth functionals to functions of bounded fractional variation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 February 2023, pp. 304-327
- Print publication:
- February 2024
-
- Article
- Export citation
Branch points for (almost-)minimizers of two-phase free boundary problems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 January 2023, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solving two-dimensional H(curl)-elliptic interface systems with optimal convergence on unfitted meshes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 774-805
-
- Article
- Export citation
On BMO and Hardy regularity estimates for a class of non-local elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 2025-2052
- Print publication:
- December 2023
-
- Article
- Export citation
EXISTENCE, UNIQUENESS AND APPROXIMATION OF SOLUTIONS TO THE STOCHASTIC LANDAU–LIFSHITZ–GILBERT EQUATION ON THE REAL LINE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 02 December 2022, pp. 171-172
- Print publication:
- February 2023
-
- Article
-
- You have access
- HTML
- Export citation
Existence and stability of singular patterns in a fractional Ginzburg–Landau equation with a mean field
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 1242-1268
-
- Article
-
- You have access
- Open access
- HTML
- Export citation