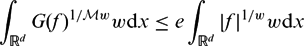Refine listing
Actions for selected content:
1821 results in 60Gxx
Asymptotic normality of degree counts in a preferential attachment model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 283-299
- Print publication:
- July 2016
-
- Article
- Export citation
Probabilistic aspects of critical growth-fragmentation equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 37-61
- Print publication:
- July 2016
-
- Article
- Export citation
Space‒time max-stable models with spectral separability
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 77-97
- Print publication:
- July 2016
-
- Article
- Export citation
On the weak limit law of the maximal uniform k-spacing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 235-238
- Print publication:
- July 2016
-
- Article
- Export citation
More on hypergeometric Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 153-158
- Print publication:
- July 2016
-
- Article
- Export citation
The sound of silence: equilibrium filtering and optimal censoring in financial markets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 119-144
- Print publication:
- July 2016
-
- Article
- Export citation
The extremogram and the cross-extremogram for a bivariate GARCH(1, 1) process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 217-233
- Print publication:
- July 2016
-
- Article
- Export citation
Coupling the Kolmogorov diffusion: maximality and efficiency considerations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 15-35
- Print publication:
- July 2016
-
- Article
- Export citation
INVARIANT MEASURES CONCENTRATED ON COUNTABLE STRUCTURES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 28 June 2016, e17
-
- Article
-
- You have access
- Open access
- Export citation
SHARP WEIGHTED BOUNDS FOR GEOMETRIC MAXIMAL OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 533-547
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Momentum liquidation under partial information
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 341-359
- Print publication:
- June 2016
-
- Article
- Export citation
Population models at stochastic times
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 481-498
- Print publication:
- June 2016
-
- Article
- Export citation
Probabilistic cellular automata with general alphabets possessing a Markov chain as an invariant distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 369-391
- Print publication:
- June 2016
-
- Article
- Export citation
Extremes for the inradius in the Poisson line tessellation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 544-573
- Print publication:
- June 2016
-
- Article
- Export citation
Stability of multiclass queueing networks under longest-queue and longest-dominating-queue scheduling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 421-433
- Print publication:
- June 2016
-
- Article
- Export citation
Planar tessellations that have the half-Gilbert structure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 574-584
- Print publication:
- June 2016
-
- Article
- Export citation
Sparre Andersen identity and the last passage time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 600-605
- Print publication:
- June 2016
-
- Article
- Export citation
A household SIR epidemic model incorporating time of day effects
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 489-501
- Print publication:
- June 2016
-
- Article
- Export citation
Shape theorems for Poisson hail on a bivariate ground
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 525-543
- Print publication:
- June 2016
-
- Article
- Export citation
Maximizing the variance of the time to ruin in a multiplayer game with selection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 610-630
- Print publication:
- June 2016
-
- Article
- Export citation