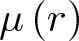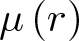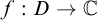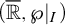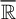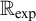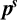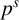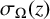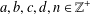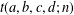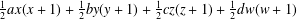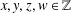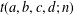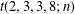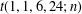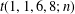Refine listing
Actions for selected content:
40 results in 33Exx
HALPHEN AND THE ELLIPTIC FUNCTIONS OF DU VAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 12 December 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRANSFORMATION FORMULA OF DWORK’S p-ADIC HYPERGEOMETRIC FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 30 October 2025, pp. 1-12
-
- Article
- Export citation
Theory of heat equations for sigma functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 February 2025, pp. 365-422
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ANALOGUE OF AN IDENTITY OF JACOBI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 07 February 2025, pp. 528-535
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic hyperlogarithms
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 January 2025, pp. 1-36
-
- Article
- Export citation
Series expansion, higher-order monotonicity properties and inequalities for the modulus of the Grötzsch ring
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 16-43
-
- Article
- Export citation
Inhomogeneous isotropic quantum spin chain associated with the difference Lamé equation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NONDEFINABILITY RESULTS FOR ELLIPTIC AND MODULAR FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GHOSTS AND CONGRUENCES FOR
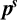 $\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
$\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 02 August 2023, pp. 96-127
-
- Article
- Export citation
JACOBIAN ELLIPTIC FUNCTIONS IN SIGNATURE FOUR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 110-124
- Print publication:
- February 2024
-
- Article
- Export citation
ON THE NUMBER OF ALGEBRAIC POINTS ON THE GRAPH OF THE WEIERSTRASS SIGMA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 205-216
- Print publication:
- October 2023
-
- Article
- Export citation
Effective rigid analytic trivializations for Drinfeld modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 20 April 2022, pp. 713-742
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A restaurant process with cocktail bar and relations to the three-parameter Mittag–Leffler distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 978-1006
- Print publication:
- December 2021
-
- Article
- Export citation
On the initial value problem for a class of nonlinear biharmonic equation with time-fractional derivative
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 26 August 2021, pp. 989-1031
- Print publication:
- August 2022
-
- Article
- Export citation
q-DISCRETE PAINLEVÉ EQUATIONS: THEIR HIERARCHIES AND PROPERTIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 14 September 2020, pp. 333-334
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
ON A LATTICE GENERALISATION OF THE LOGARITHM AND A DEFORMATION OF THE DEDEKIND ETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 118-125
- Print publication:
- August 2020
-
- Article
-
- You have access
- Open access
- Export citation
GENERALIZED FINITE POLYLOGARITHMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 19 February 2020, pp. 66-80
-
- Article
-
- You have access
- Export citation
TRANSFORMATION FORMULAS FOR THE NUMBER OF REPRESENTATIONS OF
 $n$ BY LINEAR COMBINATIONS OF FOUR TRIANGULAR NUMBERS
$n$ BY LINEAR COMBINATIONS OF FOUR TRIANGULAR NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 39-49
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
A MAGNETIC DOUBLE INTEGRAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 9-25
-
- Article
-
- You have access
- Open access
- Export citation
RAMANUJAN SERIES WITH A SHIFT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 23 October 2018, pp. 367-380
-
- Article
-
- You have access
- Export citation