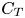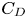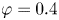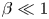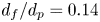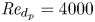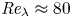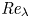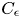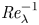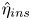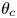Open access
Contents
JFM Papers
High-Rayleigh-number convection in porous–fluid layers
-
- Published online by Cambridge University Press:
- 14 June 2021, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effect of micromagnetorotation on magnetohydrodynamic Poiseuille micropolar flow: analytical solutions and stability analysis
-
- Published online by Cambridge University Press:
- 11 June 2021, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear stability analysis of two fluid columns of different densities and viscosities in a gravity field
-
- Published online by Cambridge University Press:
- 11 June 2021, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On non-uniqueness of the mesoscale eddy diffusivity
-
- Published online by Cambridge University Press:
- 11 June 2021, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Aerofoil wake-induced transition characteristics on a flat-plate boundary layer
-
- Published online by Cambridge University Press:
- 11 June 2021, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effect of surfactant on the linear stability of a shear-imposed fluid flowing down a compliant substrate
-
- Published online by Cambridge University Press:
- 10 June 2021, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Information transfer between turbulent boundary layers and porous media
-
- Published online by Cambridge University Press:
- 10 June 2021, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Faster Taylor bubbles
-
- Published online by Cambridge University Press:
- 08 June 2021, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Second-order adjoint-based sensitivity for hydrodynamic stability and control
-
- Published online by Cambridge University Press:
- 08 June 2021, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformation and relaxation of viscous thin films under bouncing drops
-
- Published online by Cambridge University Press:
- 04 June 2021, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Acoustic flow in porous media
-
- Published online by Cambridge University Press:
- 04 June 2021, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Residual streaming flows in buoyancy-driven cross-shore exchange
-
- Published online by Cambridge University Press:
- 04 June 2021, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
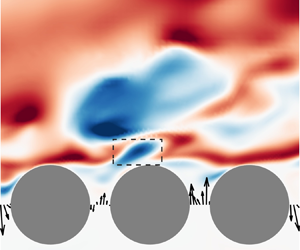
On the turbulent flow past a realistic open-cell metal foam
-
- Published online by Cambridge University Press:
- 04 June 2021, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
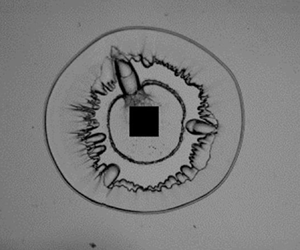
Rayleigh–Taylor instability of cylindrical water droplet induced by laser-produced cavitation bubble
-
- Published online by Cambridge University Press:
- 03 June 2021, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The viscous sublayer in front of a wall-mounted cylinder
-
- Published online by Cambridge University Press:
- 02 June 2021, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a toroidal method to solve the sessile-drop oscillation problem
-
- Published online by Cambridge University Press:
- 02 June 2021, A39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting the momentary stability analysis of the Stokes boundary layer
-
- Published online by Cambridge University Press:
- 01 June 2021, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterizing the turbulent drag properties of rough surfaces with a Taylor–Couette set-up
-
- Published online by Cambridge University Press:
- 01 June 2021, A45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A numerical and theoretical study of wind over fast-propagating water waves
-
- Published online by Cambridge University Press:
- 01 June 2021, A38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower bounds on zonal enstrophy
-
- Published online by Cambridge University Press:
- 27 May 2021, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation