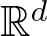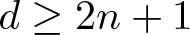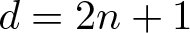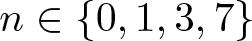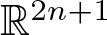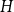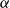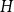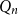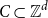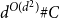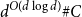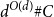Refine search
Actions for selected content:
25816 results in Abstract analysis
Structure of generalized Yamabe solitons and its applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 336-348
-
- Article
- Export citation
Optimal inverse problems of potentials for two given eigenvalues of Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1914-1937
- Print publication:
- October 2025
-
- Article
- Export citation
AN EFFECTIVE UPPER BOUND FOR ANTI-CANONICAL VOLUMES OF SINGULAR FANO THREEFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 2631-2646
- Print publication:
- November 2024
-
- Article
- Export citation
Unit sphere fibrations in Euclidean space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 287-298
-
- Article
- Export citation
Proof of some conjectural congruences involving Apéry and Apéry-like numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 508-527
-
- Article
- Export citation
Index estimates of compact hypersurfaces in smooth metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1895-1913
- Print publication:
- October 2025
-
- Article
- Export citation
Antidirected subgraphs of oriented graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 446-466
-
- Article
- Export citation
Large monochromatic components in expansive hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 467-483
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRM volume 154 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. b1-b2
- Print publication:
- April 2024
-
- Article
-
- You have access
- Export citation
A class of graphs of zero Turán density in a hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 404-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRM volume 154 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. f1-f2
- Print publication:
- April 2024
-
- Article
-
- You have access
- Export citation
Sharp bounds for a discrete John’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 484-486
-
- Article
- Export citation
Invariant measures and large deviation principles for stochastic Schrödinger delay lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1813-1854
- Print publication:
- October 2025
-
- Article
- Export citation
Bifurcations and pattern formation in a host–parasitoid model with nonlocal effect
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1855-1894
- Print publication:
- October 2025
-
- Article
- Export citation
ENERGY BOUNDS FOR MODULAR ROOTS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1765-1806
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JMJ volume 23 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. b1-b2
- Print publication:
- March 2024
-
- Article
-
- You have access
- Export citation
JMJ volume 23 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. f1-f2
- Print publication:
- March 2024
-
- Article
-
- You have access
- Export citation
On a critical time-harmonic Maxwell equation in nonlocal media
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1747-1791
- Print publication:
- October 2025
-
- Article
- Export citation
PEM series 2 volume 67 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
PEM series 2 volume 67 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation