Refine listing
Actions for selected content:
39 results in 16Pxx
GK DIMENSION AND LOCALLY NILPOTENT SKEW DERIVATIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 555-567
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Gelfand–Kirillov dimension of differential difference algebras
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 485-495
-
- Article
-
- You have access
- Export citation
ON THE REGULAR DIGRAPH OF IDEALS OF COMMUTATIVE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 16 October 2012, pp. 177-189
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Some projective surfaces of GK-dimension 4
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1195-1237
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
Nil algebras with restricted growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 461-475
-
- Article
-
- You have access
- Export citation
BOUNDED AND FULLY BOUNDED MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 04 October 2011, pp. 433-440
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
A UNIFIED APPROACH TO VARIOUS GENERALIZATIONS OF ARMENDARIZ RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 23 February 2010, pp. 361-397
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
NILPOTENCY OF THE GROUP OF UNITS OF A FINITE RING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 26 February 2009, pp. 177-182
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Characterizing rings by a direct decomposition property of their modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 359-366
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
A General Approach to the Fitting Lemma
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 155-160
- Print publication:
- December 2005
-
- Article
- Export citation
Rings in which certain right ideals are direct summands of annihilators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-346
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Goldie dimensions of quotient modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-19
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Growth of linear semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 18-30
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
Finite Generation of the Extension Algebra Ext
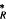 (M, M)
(M, M)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-374
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
Classes of modules with many direct summands
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 8-19
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
Symbolic powers and local cohomology
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 182-187
- Print publication:
- June 1995
-
- Article
- Export citation
Artinian band sums of rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 66-72
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Representation extensions and amalgamation bases in rings
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 394-400
- Print publication:
- December 1994
-
- Article
- Export citation
On the relation type of large powers of an ideal
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 209-214
- Print publication:
- June 1994
-
- Article
- Export citation
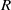
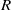
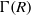
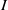
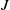
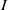
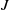
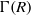
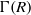
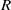
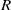
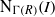
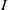
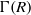
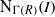
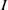
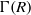
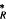 (M, M)
(M, M)
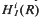 , and the comparison of the topologies defined by the
, and the comparison of the topologies defined by the