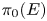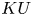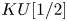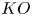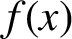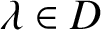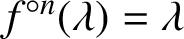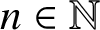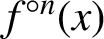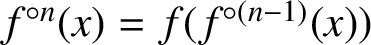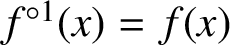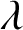Refine listing
Actions for selected content:
643 results in 16xxx
AS-REGULARITY OF GEOMETRIC ALGEBRAS OF PLANE CUBIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 22 June 2021, pp. 193-217
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
Counterexamples to Hochschild-Kostant-Rosenberg in characteristic p
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 22 June 2021, e49
-
- Article
-
- You have access
- Open access
- Export citation
REPRESENTATION VARIETIES OF ALGEBRAS WITH NODES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 2215-2245
- Print publication:
- November 2022
-
- Article
- Export citation
Brauer groups and Galois cohomology of commutative ring spectra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 1211-1264
- Print publication:
- June 2021
-
- Article
- Export citation
SIMPLICITY CRITERIA FOR RINGS OF DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 347-351
- Print publication:
- May 2022
-
- Article
- Export citation
Report on the finiteness of silting objects
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 07 May 2021, pp. 217-233
-
- Article
- Export citation
Two theorems on balanced braces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 05 May 2021, pp. 262-278
-
- Article
- Export citation
THE METRIC DIMENSION OF THE ANNIHILATING-IDEAL GRAPH OF A FINITE COMMUTATIVE RING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 27 April 2021, pp. 362-368
- Print publication:
- June 2021
-
- Article
- Export citation
On certain Tannakian categories of integrable connections over Kähler manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 21 April 2021, pp. 1034-1061
- Print publication:
- August 2022
-
- Article
- Export citation
Uniconnected solutions to the Yang–Baxter equation arising from self-maps of groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 225-233
- Print publication:
- March 2022
-
- Article
- Export citation
The Plectic Weight Filtration on Cohomology of Shimura Varieties and Partial Frobenius
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 12 April 2021, e30
-
- Article
-
- You have access
- Open access
- Export citation
Centrification of algebras and Hopf algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 155-169
- Print publication:
- March 2022
-
- Article
- Export citation
Maximal prime homomorphic images of mod-p Iwasawa algebras
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 05 March 2021, pp. 387-419
- Print publication:
- September 2021
-
- Article
- Export citation
On dualizability of braided tensor categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 09 March 2021, pp. 435-483
- Print publication:
- March 2021
-
- Article
- Export citation
Depth-graded motivic multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 22 March 2021, pp. 529-572
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FIXED POINTS OF POLYNOMIALS OVER DIVISION RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 01 March 2021, pp. 256-262
- Print publication:
- October 2021
-
- Article
- Export citation
A multiplicative dual of nil-clean rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 39-43
- Print publication:
- March 2022
-
- Article
- Export citation
Representability and autoequivalence groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 08 February 2021, pp. 657-668
- Print publication:
- November 2021
-
- Article
- Export citation
McKay matrices for finite-dimensional Hopf algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2021, pp. 686-731
- Print publication:
- June 2022
-
- Article
- Export citation
COMPLETELY PRIME ONE-SIDED IDEALS IN SKEW POLYNOMIAL RINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 03 February 2021, pp. 114-121
- Print publication:
- January 2022
-
- Article
- Export citation