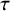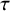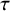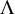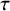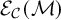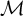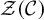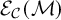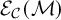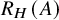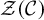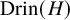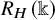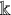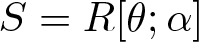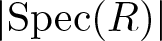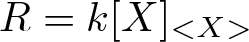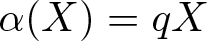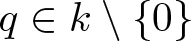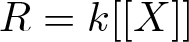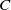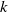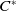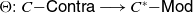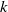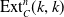Refine listing
Actions for selected content:
643 results in 16xxx
Partial Hopf actions on generalized matrix algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 26 November 2025, pp. 1-22
-
- Article
- Export citation
Reflexive homology and involutive Hochschild homology as equivariant Loday constructions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Signature maps from positive cones on algebras with involution
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 November 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moduli of objects in finite length abelian categories
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Silting, cosilting and extensions of commutative rings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Heaps of modules: categorical aspects
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 06 October 2025, e166
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the central exponent of superalgebras with superinvolution
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 September 2025, pp. 1-18
-
- Article
- Export citation
On integral decomposition of unipotent elements in integral group rings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum: “On the representability of actions of Leibniz algebras and Poisson algebras”
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1419-1420
-
- Article
-
- You have access
- HTML
- Export citation
The algebraic structure of Dyson–Schwinger equations with multiple insertion places
- Part of
-
- Journal:
- Canadian Mathematical Communications / Volume 1 / 2025
- Published online by Cambridge University Press:
- 29 August 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FROBENIUS-PERRON DIMENSIONS OF CONJUGACY CLASSES AND AN ITO-MICHLER-TYPE RESULT IN MODULAR FUSION CATEGORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 28 August 2025, pp. 2523-2542
- Print publication:
- November 2025
-
- Article
- Export citation
Operator realizations of non-commutative analytic functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 August 2025, e137
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Colored interacting particle systems on the ring: Stationary measures from Yang–Baxter equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1855-1922
- Print publication:
- August 2025
-
- Article
- Export citation
G-dimensions for DG-modules over commutative DG-rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1370-1389
-
- Article
- Export citation
Mutation graph of support
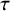 $\tau $-tilting modules over a skew-gentle algebra
$\tau $-tilting modules over a skew-gentle algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Consistent dimer models on surfaces with boundary
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FISHING FOR COMPLEMENTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reflective centers of module categories and quantum K-matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 June 2025, e95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Property (◇) for Ore extensions of small Krull dimension
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1169-1187
-
- Article
- Export citation
Homological full-and-faithfulness of comodule inclusion and contramodule forgetful functors
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation