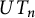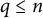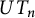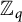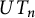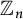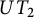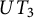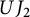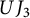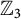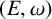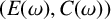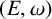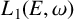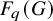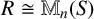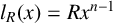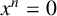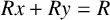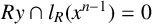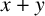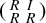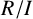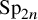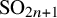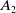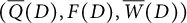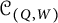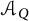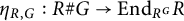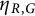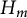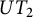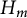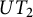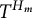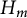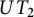Refine listing
Actions for selected content:
643 results in 16xxx
Images of multilinear graded polynomials on upper triangular matrix algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 1540-1565
- Print publication:
- October 2023
-
- Article
- Export citation
LEAVITT PATH ALGEBRAS OF WEIGHTED AND SEPARATED GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 1-25
- Print publication:
- August 2023
-
- Article
- Export citation
CORRIGENDUM TO “CLUSTER CATEGORIES FROM GRASSMANNIANS AND ROOT COMBINATORICS”
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 269-273
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WHEN IS A COMPLETION OF THE UNIVERSAL ENVELOPING ALGEBRA A BANACH PI-ALGEBRA?
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 493-501
- Print publication:
- June 2023
-
- Article
- Export citation
A BRICK VERSION OF A THEOREM OF AUSLANDER
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 88-106
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability conditions for contraction algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A categorical approach to dynamical quantum groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CHARACTERISATION OF MATRIX RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 08 August 2022, pp. 95-101
- Print publication:
- February 2023
-
- Article
- Export citation
Calabi–Yau properties of Postnikov diagrams
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 July 2022, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-solvable lattice models for
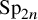 $\operatorname {Sp}_{2n}$ and
$\operatorname {Sp}_{2n}$ and 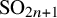 $\operatorname {SO}_{2n+1}$ Demazure atoms and characters
$\operatorname {SO}_{2n+1}$ Demazure atoms and characters
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 July 2022, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Graded comodule categories with enough projectives
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 257-271
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A conjecture strengthening the Zariski dense orbit problem for birational maps of dynamical degree one
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 477-491
- Print publication:
- June 2023
-
- Article
- Export citation
On the computation of Hopf 2-cocycles with an example of diagonal type
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 141-169
- Print publication:
- January 2023
-
- Article
- Export citation
Quivers with potentials for Grassmannian cluster algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 1199-1225
- Print publication:
- August 2023
-
- Article
- Export citation
Corrigendum: Liftings of Jordan and Super Jordan Planes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 577-586
-
- Article
-
- You have access
- HTML
- Export citation
Auslander’s theorem for dihedral actions on preprojective algebras of type A
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 324-339
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cluster categories of formal DG algebras and singularity categories
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 08 June 2022, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Totally nonnegative Grassmannians, Grassmann necklaces, and quiver Grassmannians
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 03 June 2022, pp. 1076-1109
- Print publication:
- August 2023
-
- Article
- Export citation
CELLULAR CATEGORIES AND STABLE INDEPENDENCE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 May 2022, pp. 811-834
- Print publication:
- June 2023
-
- Article
- Export citation
Specht property for the algebra of upper triangular matrices of size two with a Taft’s algebra action
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 16 May 2022, pp. 303-323
- Print publication:
- March 2023
-
- Article
- Export citation