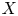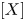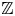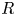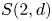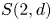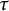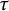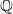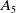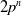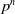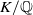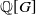Refine listing
Actions for selected content:
643 results in 16xxx
Graded extensions of Verma modules
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 08 November 2024, pp. 285-311
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Laurent family of simple modules over quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1916-1940
- Print publication:
- August 2024
-
- Article
- Export citation
Fiber functors and reconstruction of Hopf algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1718-1761
- Print publication:
- October 2025
-
- Article
- Export citation
Pieri rules for skew dual immaculate functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 29 April 2024, pp. 902-914
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topologically free actions and ideals in twisted Banach algebra crossed products
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-31
-
- Article
- Export citation
The Waring problem for upper triangular matrix algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1398-1424
- Print publication:
- August 2025
-
- Article
- Export citation
Quasi-hereditary covers of Temperley–Lieb algebras and relative dominant dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Skew group categories, algebras associated to Cartan matrices and folding of root lattices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 01 April 2024, pp. 2240-2284
- Print publication:
- December 2025
-
- Article
- Export citation
WHEN IS THE SILTING-DISCRETENESS INHERITED?
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 01 April 2024, pp. 905-927
- Print publication:
- December 2024
-
- Article
- Export citation
On the structure of some one-generator braces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 566-576
-
- Article
- Export citation
Finite skew braces of square-free order and supersolubility
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 March 2024, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On tau-tilting subcategories
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 March 2024, pp. 975-1012
- Print publication:
- June 2025
-
- Article
- Export citation
IDEMPOTENT GENERATORS OF INCIDENCE ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 488-497
- Print publication:
- December 2024
-
- Article
- Export citation
Log Calabi–Yau surfaces and Jeffrey–Kirwan residues
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 547-592
- Print publication:
- May 2024
-
- Article
- Export citation
A NOTE ON PROJECTIONS IN ÉTALE GROUPOID ALGEBRAS AND DIAGONAL-PRESERVING HOMOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 508-513
- Print publication:
- December 2024
-
- Article
- Export citation
On twisted group ring isomorphism problem for p-groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 368-381
- Print publication:
- May 2024
-
- Article
- Export citation
GRAPH CHARACTERISATION OF THE ANNIHILATOR IDEALS OF LEAVITT PATH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 498-507
- Print publication:
- December 2024
-
- Article
- Export citation
Leopoldt-type theorems for non-abelian extensions of
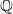 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 January 2024, pp. 308-337
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COEFFICIENT QUIVERS,
 ${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 561-617
- Print publication:
- September 2024
-
- Article
- Export citation
Graphical methods and rings of invariants on the symmetric algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2173-2198
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation