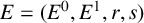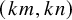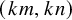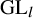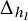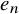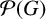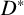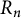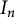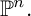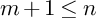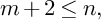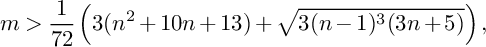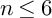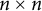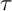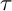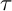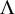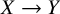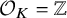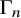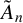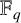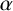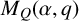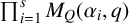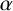Refine listing
Actions for selected content:
643 results in 16xxx
SIMPLICITY OF LEAVITT PATH ALGEBRAS VIA GRADED RING THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 03 March 2023, pp. 428-437
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boolean algebras, Morita invariance and the algebraic K-theory of Lawvere theories
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 253-270
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Shuffle Theorem for Paths Under Any Line
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 22 February 2023, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Proof of the Extended Delta Conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 22 February 2023, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CATEGORIFICATION OF ACYCLIC PRINCIPAL COEFFICIENT CLUSTER ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 22 February 2023, pp. 769-809
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SEMIRING AND INVOLUTION IDENTITIES OF POWER GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 17 January 2023, pp. 354-374
- Print publication:
- December 2023
-
- Article
- Export citation
A NOTE ON SUBNORMAL SUBGROUPS IN DIVISION RINGS CONTAINING SOLVABLE SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 422-427
- Print publication:
- December 2023
-
- Article
- Export citation
Quasisymmetric harmonics of the exterior algebra
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 January 2023, pp. 997-1013
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANNIHILATORS AND DIMENSIONS OF THE SINGULARITY CATEGORY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 06 January 2023, pp. 533-548
- Print publication:
- June 2023
-
- Article
- Export citation
GENERIC LINES IN PROJECTIVE SPACE AND THE KOSZUL PROPERTY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 06 January 2023, pp. 576-605
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Norms on complex matrices induced by random vectors
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 23 December 2022, pp. 808-826
- Print publication:
- September 2023
-
- Article
- Export citation
Homological approximations in persistence theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 12 December 2022, pp. 66-103
- Print publication:
- February 2024
-
- Article
- Export citation
Riemann–Roch for stacky matrix factorizations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 06 December 2022, e108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The flow tree formula for Donaldson–Thomas invariants of quivers with potentials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 19 December 2022, pp. 2206-2249
- Print publication:
- December 2022
-
- Article
- Export citation
Twisted algebras of geometric algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 715-730
- Print publication:
- September 2023
-
- Article
- Export citation
AUTOMORPHISMS AND SYMPLECTIC LEAVES OF CALOGERO–MOSER SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 26-57
- Print publication:
- August 2023
-
- Article
- Export citation
MINIMAL (
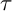 $\tau $-)TILTING INFINITE ALGEBRAS
$\tau $-)TILTING INFINITE ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 11 October 2022, pp. 221-238
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computation of lattice isomorphisms and the integral matrix similarity problem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Euler continuants in noncommutative quasi-Poisson geometry
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CANONICAL DECOMPOSITION AND QUIVER REPRESENTATIONS OF TYPE
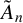 $\tilde {A}_n$ OVER FINITE FIELDS
$\tilde {A}_n$ OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 250-260
- Print publication:
- April 2023
-
- Article
- Export citation