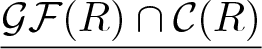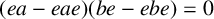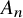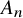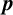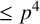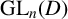Refine listing
Actions for selected content:
643 results in 16xxx
Products of commutators in matrix rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 14 January 2025, pp. 512-529
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Locally finitely presented Grothendieck categories and the pure semisimplicity conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-27
-
- Article
- Export citation
From actions of an abelian group on itself to left braces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 65-79
- Print publication:
- January 2025
-
- Article
- Export citation
Addenda to “Correspondence theorems for Hopf algebroids with applications to affine groupoids”
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 347-350
- Print publication:
- February 2025
-
- Article
- Export citation
A note on right-nil and strong-nil skew braces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-9
-
- Article
- Export citation
A McKay Correspondence in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On split quasi-hereditary covers and Ringel duality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e105
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GV and GW invariants via the enhanced movable cone
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enlargements and Morita contexts for rings with involution
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 131-162
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Model structures, n-Gorenstein flat modules and PGF dimensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1241-1264
-
- Article
- Export citation
RADICALS AND IDEMPOTENTS III: q-CENTRAL IDEMPOTENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 272-282
- Print publication:
- April 2025
-
- Article
- Export citation
The socle of subshift algebras, with applications to subshift conjugacy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-26
-
- Article
- Export citation
A smooth compactification of spaces of stability conditions: the case of the
 $A_{n}$-quiver
$A_{n}$-quiver
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 November 2024, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simplicity of non-associative skew Laurent polynomial rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RATIONAL REPRESENTATIONS AND RATIONAL GROUP ALGEBRA OF VZ
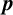 $\boldsymbol {p}$-GROUPS
$\boldsymbol {p}$-GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1-30
- Print publication:
- February 2025
-
- Article
- Export citation
LOCALLY NILPOTENT SUBGROUPS OF
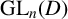 $\mathrm {GL}_n(D)$
$\mathrm {GL}_n(D)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 128-138
- Print publication:
- August 2025
-
- Article
- Export citation
Tachikawa's second conjecture, derived recollements, and gendo-symmetric algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 27 December 2024, pp. 2704-2737
- Print publication:
- November 2024
-
- Article
- Export citation
Resolving dualities and applications to homological invariants
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 22 October 2024, pp. 1861-1889
- Print publication:
- December 2025
-
- Article
- Export citation
QUASI-HEREDITARY SKEW GROUP ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 24 September 2024, pp. 1-44
- Print publication:
- March 2025
-
- Article
- Export citation
DT INVARIANTS FROM VERTEX ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 September 2024, pp. 291-339
- Print publication:
- January 2025
-
- Article
- Export citation


















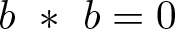
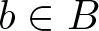





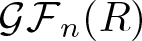
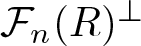

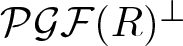

 . The homotopy category of this model structure is triangulated equivalent to the stable category
. The homotopy category of this model structure is triangulated equivalent to the stable category