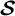 $\mathcal{\textbf{S}}$
-adic characterization of minimal ternary dendric shifts
$\mathcal{\textbf{S}}$
-adic characterization of minimal ternary dendric shifts
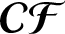 $\boldsymbol{\mathcal{CF}}$
-CONNECTED GRAPHS FOR
$\boldsymbol{\mathcal{CF}}$
-CONNECTED GRAPHS FOR
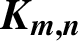 $\boldsymbol{K}_{\boldsymbol{m,n}}$
$\boldsymbol{K}_{\boldsymbol{m,n}}$
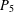 $P_{5}$, GEM)-FREE GRAPHS
$P_{5}$, GEM)-FREE GRAPHS
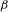 $\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
$\unicode[STIX]{x1D6FD}$-transformation with a hole at 0