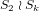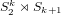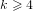Refine listing
Actions for selected content:
96 results in 52Bxx
Flow Polytopes and the Space of Diagonal Harmonics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1495-1521
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Galois theory for general systems of polynomial equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 229-245
- Print publication:
- February 2019
-
- Article
- Export citation
ARITHMETIC ASPECTS OF SYMMETRIC EDGE POLYTOPES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 14 May 2019, pp. 763-784
- Print publication:
- 2019
-
- Article
- Export citation
FLAG AREA MEASURES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 23 July 2019, pp. 958-989
- Print publication:
- 2019
-
- Article
- Export citation
Diameter, Decomposability, and Minkowski Sums of Polytopes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 741-755
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
THE LOCAL
 $h$-POLYNOMIALS OF CLUSTER SUBDIVISIONS HAVE ONLY REAL ZEROS
$h$-POLYNOMIALS OF CLUSTER SUBDIVISIONS HAVE ONLY REAL ZEROS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 258-264
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
TRIANGLES CAPTURING MANY LATTICE POINTS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 25 April 2018, pp. 551-582
- Print publication:
- 2018
-
- Article
- Export citation
AN INCLUSION–EXCLUSION IDENTITY FOR NORMAL CONES OF POLYHEDRAL SETS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 05 February 2018, pp. 124-136
- Print publication:
- 2018
-
- Article
- Export citation
NONCROSSING SETS AND A GRASSMANN ASSOCIAHEDRON
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 20 February 2017, e5
-
- Article
-
- You have access
- Open access
- Export citation
TIGHTER BOUNDS FOR THE DISCREPANCY OF BOXESAND POLYTOPES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1091-1113
- Print publication:
- 2017
-
- Article
- Export citation
A FLAG VECTOR OF A 3-SPHERE THAT IS NOT THE FLAG VECTOR OF A 4-POLYTOPE
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 08 December 2016, pp. 260-271
- Print publication:
- 2017
-
- Article
- Export citation
A Novel Efficient Numerical Solution of Poisson's Equation for Arbitrary Shapes in Two Dimensions
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 5 / November 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1381-1404
- Print publication:
- November 2016
-
- Article
- Export citation
SHAPES OF POLYHEDRA, MIXED VOLUMES AND HYPERBOLIC GEOMETRY
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 23 September 2016, pp. 124-183
- Print publication:
- 2017
-
- Article
- Export citation
The linear programming relaxation permutation symmetry group of an orthogonal array defining integer linear program
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 206-216
-
- Article
-
- You have access
- Export citation
Analysis of a Two-Level Algorithm for HDG Methods for Diffusion Problems
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1435-1460
- Print publication:
- May 2016
-
- Article
- Export citation
On the equations and classification of toric quiver varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 265-295
- Print publication:
- April 2016
-
- Article
- Export citation
DUALITY FOR QUASIPOLYTOPES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 26 February 2016, pp. 95-117
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
INTERMEDIATE SUMS ON POLYHEDRA II: BIDEGREE AND POISSON FORMULA
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 29 February 2016, pp. 653-684
- Print publication:
- 2016
-
- Article
- Export citation
LOWER BOUND THEOREMS AND A GENERALIZED LOWER BOUND CONJECTURE FOR BALANCED SIMPLICIAL COMPLEXES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 441-477
- Print publication:
- 2016
-
- Article
- Export citation
CoxIter – Computing invariants of hyperbolic Coxeter groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 754-773
-
- Article
-
- You have access
- Export citation
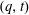
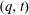
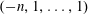
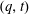
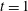
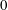
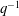
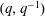
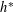

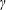
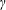

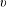
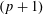
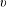
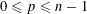
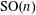
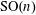
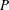
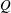
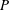
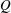
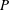
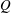
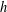
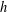
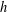
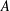
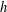
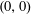
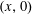
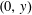
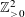
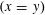
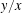
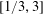
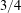
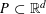
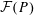
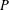
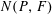
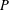
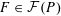
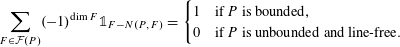
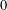
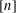
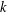
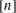
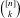
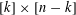
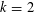
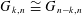

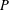
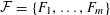
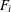
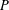

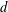
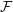
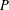
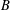
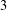
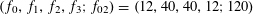
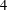
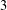
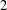
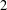
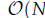 , where
, where