We show that the maximum likelihood degree of a smooth very affine variety is equal to the signed topological Euler characteristic. This generalizes Orlik and Terao’s solution to Varchenko’s conjecture on complements of hyperplane arrangements to smooth very affine varieties. For very affine varieties satisfying a genericity condition at infinity, the result is further strengthened to relate the variety of critical points to the Chern–Schwartz–MacPherson class. The strengthened version recovers the geometric deletion–restriction formula of Denham et al. for arrangement complements, and generalizes Kouchnirenko’s theorem on the Newton polytope for nondegenerate hypersurfaces.

Generalizing a result (the case $k= 1$) due to M. A. Perles, we show that any polytopal upper bound sphere of odd dimension $2k+ 1$ belongs to the generalized Walkup class ${ \mathcal{K} }_{k} (2k+ 1)$, i.e., all its vertex links are $k$-stacked spheres. This is surprising since it is far from obvious that the vertex links of polytopal upper bound spheres should have any special combinatorial structure. It has been conjectured that for $d\not = 2k+ 1$, all $(k+ 1)$-neighborly members of the class ${ \mathcal{K} }_{k} (d)$ are tight. The result of this paper shows that the hypothesis $d\not = 2k+ 1$ is essential for every value of $k\geq 1$.

We exhibit seven linear codes exceeding the current best known minimum distance $d$ for their dimension $k$ and block length $n$. Each code is defined over ${ \mathbb{F} }_{8} $, and their invariants $[n, k, d] $ are given by $[49, 13, 27] $, $[49, 14, 26] $, $[49, 16, 24] $, $[49, 17, 23] $, $[49, 19, 21] $, $[49, 25, 16] $ and $[49, 26, 15] $. Our method includes an exhaustive search of all monomial evaluation codes generated by points in the $[0, 5] \times [0, 5] $ lattice square.

We study intermediate sums, interpolating between integrals and discrete sums, which were introduced by A. Barvinok in [Computing the Ehrhart quasi-polynomial of a rational simplex. Math. Comp. 75 (2006), 1449–1466]. For a given polytope 𝔭 with facets parallel to rational hyperplanes and a rational subspace L, we integrate a given polynomial function h over all lattice slices of the polytope 𝔭 parallel to the subspace L and sum up the integrals. We first develop an algorithmic theory of parametric intermediate generating functions. Then we study the Ehrhart theory of these intermediate sums, that is, the dependence of the result as a function of a dilation of the polytope. We provide an algorithm to compute the resulting Ehrhart quasi-polynomials in the form of explicit step-polynomials. These formulas are naturally valid for real (not just integer) dilations and thus provide a direct approach to real Ehrhart theory.

We raise and investigate the following problem which one can regard as a very close relative of the densest sphere packing problem. If the Euclidean 3-space is partitioned into convex cells each containing a unit ball, how should the shapes of the cells be designed to minimize the average surface area of the cells? In particular, we prove that the average surface area in question is always at least

We consider the convex hull ℬk of the symmetric moment curve Uk(t)=(cos t,sin t,cos 3t,sin 3t,…,cos (2k−1)t,sin (2k−1)t) in ℝ2k, where t ranges over the unit circle 𝕊=ℝ/2πℤ. The curve Uk(t) is locally neighborly: as long as t1,…,tk lie in an open arc of 𝕊 of a certain length ϕk>0 , the convex hull of the points Uk (t1),…,Uk (tk)is a face of ℬk. We characterize the maximum possible length ϕk, proving, in particular, that ϕk >π/2for all k and that the limit of ϕk is π/2as k grows. This allows us to construct centrally symmetric polytopes with a record number of faces.

Tessellations of R3 that use convex polyhedral cells to fill the space can be extremely complicated. This is especially so for tessellations which are not ‘facet-to-facet’, that is, for those where the facets of a cell do not necessarily coincide with the facets of that cell's neighbours. Adjacency concepts between neighbouring cells (or between neighbouring cell elements) are not easily formulated when facets do not coincide. In this paper we make the first systematic study of these topological relationships when a tessellation of R3 is not facet-to-facet. The results derived can also be applied to the simpler facet-to-facet case. Our study deals with both random tessellations and deterministic ‘tilings’. Some new theory for planar tessellations is also given.

For a d-dimensional convex lattice polytope P, a formula for the boundary volume vol(∂P) is derived in terms of the number of boundary lattice points on the first ⌊d/2⌋ dilations of P. As an application we give a necessary and sufficient condition for a polytope to be reflexive, and derive formulas for the f-vector of a smooth polytope in dimensions three, four, and five. We also give applications to reflexive order polytopes, and to the Birkhoff polytope.

This article considers a family of functionals J to be maximized over the planar convex sets K for which the perimeter and Steiner point have been fixed. Assuming that J is the integral of a positive quadratic expression in the support function h and its derivative, the maximizer is always either a triangle or a line segment (which can be considered as a collapsed triangle). Among the concrete consequences of the main theorem is the fact that, given any convex body K1 of finite perimeter, the set in this class that is farthest away in the sense of the L2 distance is always a line segment. The same property is proved for the Hausdorff distance.

We realize the multiplihedron geometrically as the moduli space of stable quilted disks. This generalizes the geometric realization of the associahedron as the moduli space of stable disks. We show that this moduli space is the non-negative real part of a complex moduli space of stable scaled marked curves.

Toric log del Pezzo surfaces correspond to convex lattice polygons containing the origin in their interior and having only primitive vertices. Upper bounds on the volume and on the number of boundary lattice points of these polygons are derived in terms of the index ℓ. Techniques for classifying these polygons are also described: a direct classification for index two is given, and a classification for all ℓ≤16 is obtained.

Viro method plays an important role in the study of topology of real algebraic hypersurfaces. The T-primitive hypersurfaces we study here appear as the result of Viro's combinatorial patchworking when one starts with a primitive triangulation. We show that the Euler characteristic of the real part of such a hypersurface of even dimension is equal to the signature of its complex part. We explain how this can be understood in tropical geometry. We use this result to prove the existence of maximal surfaces in some three-dimensional toric varieties, namely those corresponding to Nakajima polytopes.

The face ring of a homology manifold (without boundary) modulo a generic system of parameters is studied. Its socle is computed and it is verified that a particular quotient of this ring is Gorenstein. This fact is used to prove that the algebraic g-conjecture for spheres implies all enumerative consequences of its far-reaching generalization (due to Kalai) to manifolds. A special case of Kalai’s conjecture is established for homology manifolds that have a codimension-two face whose link contains many vertices.

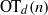
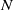
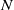
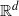
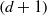
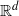
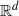
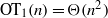
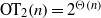
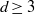
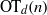
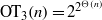
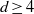
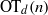
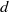
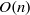
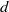
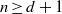
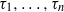
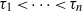
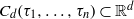
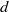
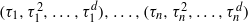
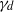
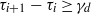
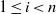
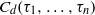
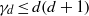
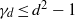
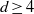
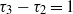
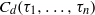
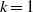
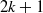
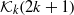
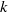
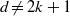
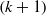
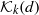
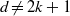
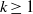
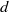
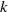
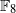
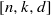
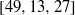
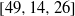
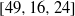
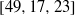
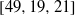
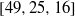
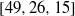
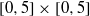
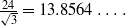
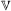Let be a finite-dimensional vector space over a square-root closed ordered field 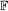(this restriction permits an inner product with corresponding norm to be imposed on ). Many properties of the family :=() of convex polytopes in can be expressed in terms of valuations (or finitely additive measures). Valuations such as volume, surface area and the Euler characteristic are translation invariant, but others, such as the moment vector and inertia tensor, display a polynomial behaviour under translation. The common framework for such valuations is the polytope (or Minkowski) ring Π:=Π(), and its quotients under various powers of the ideal T of Π which is naturally associated with translations. A central result in the theory is that, in all but one trivial respect, the ring Π/T is actually a graded algebra over . Unfortunately, while the quotients Π/Tk+1 are still graded rings for k > 1, they now only possess a rational algebra structure; to obtain an algebra over , some (weak) continuity assumptions have to be made, although these can be achieved algebraically, by factoring out a further ideal A, the algebra ideal.

The Ehrhart polynomials for the class of 0-symmetric convex lattice polytopes in Euclidean n-space ℝn are investigated. It turns out that the roots of the Ehrhart polynomial and Minkowski's successive minima of such polytopes are closely related by their geometric and arithmetic means. It is also shown that the roots of the Ehrhart polynomials of lattice n-polytopes with or without interior lattice points differ essentially. Furthermore, the structure of the roots in the planar case is studied. Here it turns out that their distribution reflects basic properties of lattice polygons.

Equifacetal simplices, all of whose codimension one faces are congruent to one another, are studied. It is shown that the isometry group of such a simplex acts transitively on its set of vertices and, as an application, equifacetal simplices are shown to have unique centres. It is conjectured that a simplex with a unique centre must be equifacetal. The notion of the combinatorial type of an equifacetal simplex is introduced and analysed, and all possible combinatorial types of equifacetal simplices are constructed in even dimensions.

Voronoĭ conjectured that every parallelotope is affinely equivalent to a Voronoĭ polytope. For some m, a parallelotope is defined by a set of m facet vectors pi, and defines a set of m lattice vectors ti, for 1≤i≤m. It is shown that Voronoĭ's conjecture is true for an n-dimensional parallelotope P if and only if there exist scalars γi, and a positive definite n × n matrix Q such that γipi = Qti for each i. In this case, the quadratic form f(x) = xTQx is the metric form of P.

It is shown that, for any lattice polytope P⊂ℝd the set int (P)∩lℤd (provided that it is non-empty) contains a point whose coefficient of asymmetry with respect to P is at most 8d · (8l+7)22d+1. If, moreover, P is a simplex, then this bound can be improved to 8 · (8l+7 )2d+1. As an application, new upper bounds on the volume of a lattice polytope are deduced, given its dimension and the number of sublattice points in its interior.

This paper is concerned with convex bodies in n-dimensional lp, spaces, where each body is accessible only by a weak separation or optimization oracle. It studies the asymptotic relative accuracy, as n→∞, of polynomial-time approximation algorithms for the diameter, width, circumradius, and inradius of a body K, and also for the maximum of the norm over K.

Consider a convex polytope X and a family of convex sets, satisfying a given property P. Moreover, assume that is closed under operations of cutting and convex pasting along hyperplanes. Necessary and sufficient conditions are given to have . As a consequence, it follows that, if all simplices or small enough simplices have the property in question, then X also has that property.