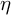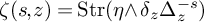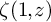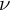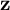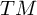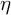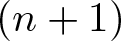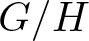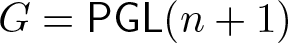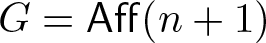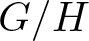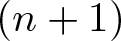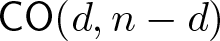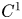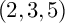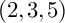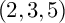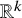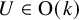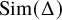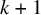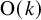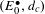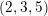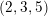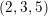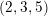Refine listing
Actions for selected content:
31 results in 58Axx
ZETA INVARIANTS OF MORSE FORMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 411-480
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projectively and affinely invariant PDEs on hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 714-739
-
- Article
- Export citation
The aromatic bicomplex for the description of divergence-free aromatic forms and volume-preserving integrators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 08 August 2023, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Involutivity of distributions at points of superdense tangency with respect to normal currents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 24 March 2023, pp. 508-524
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINES ON HOLOMORPHIC CONTACT MANIFOLDS AND A GENERALIZATION OF
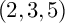 $(2,3,5)$-DISTRIBUTIONS TO HIGHER DIMENSIONS
$(2,3,5)$-DISTRIBUTIONS TO HIGHER DIMENSIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 652-668
- Print publication:
- September 2023
-
- Article
- Export citation
O-minimal de Rham Cohomology
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 16 January 2023, p. 529
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
Families of similar simplices inscribed in most smoothly embedded spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 November 2022, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nontame Morse–Smale flows and odd Chern–Weil theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 1579-1624
- Print publication:
- December 2022
-
- Article
- Export citation
ON PROJECTIVE MANIFOLDS WITH PSEUDO-EFFECTIVE TANGENT BUNDLE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1801-1830
- Print publication:
- September 2022
-
- Article
- Export citation
Hodge Representations
- Part of
-
- Journal:
- Experimental Results / Volume 1 / 2020
- Published online by Cambridge University Press:
- 17 November 2020, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POINCARÉ AND SOBOLEV INEQUALITIES FOR DIFFERENTIAL FORMS IN HEISENBERG GROUPS AND CONTACT MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 29 June 2020, pp. 869-920
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
MIXED HODGE STRUCTURES WITH MODULUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 02 March 2020, pp. 161-195
- Print publication:
- January 2022
-
- Article
- Export citation
DUALITY OF (2, 3, 5)-DISTRIBUTIONS AND LAGRANGIAN CONE STRUCTURES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 23 January 2020, pp. 303-315
- Print publication:
- September 2021
-
- Article
- Export citation
Loose Engel structures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 06 January 2020, pp. 412-434
- Print publication:
- February 2020
-
- Article
- Export citation
On Subcartesian Spaces Leibniz’ Rule Implies the Chain Rule
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 07 November 2019, pp. 348-357
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Point derivations and cohomologies of Lipschitz algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 18 July 2019, pp. 1173-1187
-
- Article
- Export citation
Analytic and geometric properties of dislocation singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1609-1651
- Print publication:
- August 2020
-
- Article
- Export citation
DIFFERENTIAL FORMS ON STRATIFIED SPACES II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 311-318
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
DIFFERENTIAL FORMS ON STRATIFIED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 13 July 2018, pp. 319-330
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
OBSTRUCTION THEORY FOR SUPERMANIFOLDS AND DEFORMATIONS OF SUPERCONFORMAL STRUCTURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 15 March 2017, pp. 512-514
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation