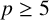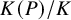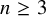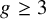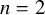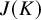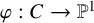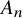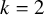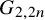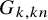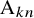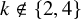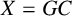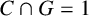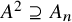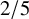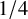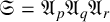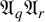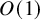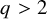Refine listing
Actions for selected content:
147 results in 20Bxx
DERANGEMENTS IN PERMUTATION GROUPS WITH TWO ORBITS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 05 December 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wreath products and the non-coprime k(GV) problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Permutation groups, partition lattices and block structures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 October 2025, e180
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MIXED IDENTITIES FOR OLIGOMORPHIC AUTOMORPHISM GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 19 August 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the quasi-transitivity degree of branch groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 04 August 2025, pp. 695-715
- Print publication:
- November 2025
-
- Article
- Export citation
On derangements in simple permutation groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 23 June 2025, e98
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Aldous-Caputo Spectral Gap Conjecture for Hypergraphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 259-298
- Print publication:
- September 2025
-
- Article
- Export citation
On the Fourier coefficients of word maps on unitary groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 681-713
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXCEPTIONAL GROUPS OF ORDER
 $p^6$ FOR PRIMES
$p^6$ FOR PRIMES 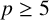 $p\geq 5$
$p\geq 5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 485-496
- Print publication:
- December 2025
-
- Article
- Export citation
A single source theorem for primitive points on curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A complete classification of shuffle groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 04 December 2024, e104
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PRODUCT OF A GENERALIZED QUATERNION GROUP AND A CYCLIC GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 31-64
- Print publication:
- February 2025
-
- Article
- Export citation
Improved covering results for conjugacy classes of symmetric groups via hypercontractivity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
VERTEX-PRIMITIVE s-ARC-TRANSITIVE DIGRAPHS OF ALMOST SIMPLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 16 October 2024, pp. 566-567
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON MINIMAL DEGREES OF QUOTIENT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 177-179
- Print publication:
- February 2025
-
- Article
-
- You have access
- HTML
- Export citation
Gassmann triples with special cycle types and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 10 October 2024, pp. 1115-1124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ENUMERATION OF GROUPS IN SOME SPECIAL VARIETIES OF A-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 27 August 2024, pp. 107-117
- Print publication:
- February 2025
-
- Article
- Export citation
Finitely generated simple sharply 2-transitive groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 September 2024, pp. 1941-1957
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hypercontractivity on the symmetric group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 January 2024, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Base sizes of primitive groups of diagonal type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 04 January 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation