Refine listing
Actions for selected content:
64 results in 20Hxx
The constructive membership problem for discrete free subgroups of rank 2 of
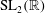 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathrm{SL}_2(\mathbb{R})$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathrm{SL}_2(\mathbb{R})$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 345-359
-
- Article
-
- You have access
- Export citation
Congruence testing for odd subgroups of the modular group
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 206-208
-
- Article
-
- You have access
- Export citation
Computing fundamental domains for the Bruhat–Tits tree for
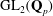 ${\rm GL}_2(\mathbf{Q}_p)$ ,
${\rm GL}_2(\mathbf{Q}_p)$ , 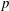 $p$ -adic automorphic forms, and the canonical embedding of Shimura curves
$p$ -adic automorphic forms, and the canonical embedding of Shimura curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 1-23
-
- Article
-
- You have access
- Export citation
A REMARK ON THE PERMUTATION REPRESENTATIONS AFFORDED BY THE EMBEDDINGS OF
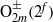 ${ \text{O} }_{2m}^{\pm } ({2}^{f} )$ IN
${ \text{O} }_{2m}^{\pm } ({2}^{f} )$ IN 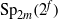 ${\text{Sp} }_{2m} ({2}^{f} )$
${\text{Sp} }_{2m} ({2}^{f} )$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 19 September 2013, pp. 331-336
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
Unipotent differential algebraic groups as parameterized differential Galois groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 671-700
- Print publication:
- October 2014
-
- Article
- Export citation
CONTINUED FRACTIONS FOR A CLASS OF TRIANGLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2013, pp. 21-42
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Computing Hall subgroups of finite groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 205-218
-
- Article
-
- You have access
- Export citation
GENERATING SYSTEMS OF SUBGROUPS IN SU(2, 1)
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 07 June 2012, pp. 346-352
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Quantifying residual finiteness of arithmetic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 907-920
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
PROPERTY (FA) OF THE GAUSS–PICARD MODULAR GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 15 March 2011, pp. 225-228
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
Primitivity testing of finite nilpotent linear groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 March 2011, pp. 87-98
-
- Article
-
- You have access
- Export citation
CONVEX STANDARD FUNDAMENTAL DOMAIN FOR SUBGROUPS OF HECKE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 96-107
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Fundamental domains for genus-zero and genus-one congruence subgroups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 July 2010, pp. 222-245
-
- Article
-
- You have access
- Export citation
ON KLEINIAN GROUPS WITH THE SAME SET OF AXES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 437-441
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
On (2, 3, 7)-generation of maximal parabolic subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-200
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
On real forms of a complex algebraic curve
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 134-142
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
Commutators in pseudo-orthogonal groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 353-365
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
Cusps, triangle groups and hyperbolic 3-folds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-182
- Print publication:
- October 1993
-
- Article
-
- You have access
- Export citation
Factorization of invertible matrices over rings of stable rank one
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 3 / June 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 455-460
- Print publication:
- June 1990
-
- Article
-
- You have access
- Export citation
Classical groups and generalized simple groups of Lie type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 53-70
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
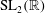
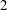
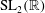
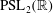
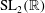
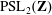
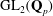
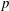
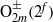
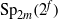
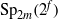
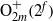
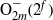
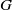
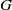
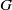
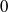
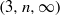
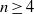
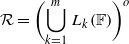
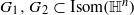 with the same set of axes are commensurable. We give some partial solutions.
with the same set of axes are commensurable. We give some partial solutions.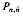 of
of 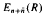 consisting of the matrices of shape
consisting of the matrices of shape 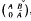 , where
, where 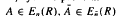 and
and 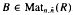 , is (2, 3, 7)-generated whenever
, is (2, 3, 7)-generated whenever 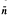 are large enough.
are large enough.