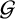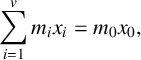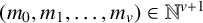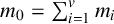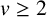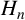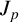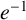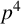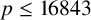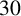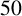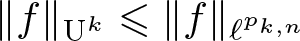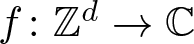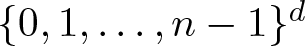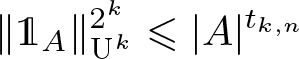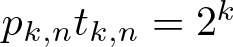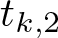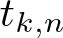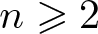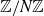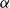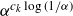Refine listing
Actions for selected content:
343 results in 11Bxx
ON A PROBLEM OF NATHANSON ON NONMINIMAL ADDITIVE COMPLEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 15 December 2025, pp. 1-8
-
- Article
- Export citation
Quantitative bounds in a popular polynomial Szemerédi theorem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 December 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explicit sumset sizes in additive number theory
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Large Salem sets avoiding nonlinear configurations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 November 2025, pp. 1-46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ADDITIVE COMPLEMENTS IN THE COMPLEMENT OF A SET OF NATURAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 November 2025, pp. 1-13
-
- Article
- Export citation
Local aspects of the Sidorenko property for linear equations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 23 October 2025, e177
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUANTITATIVE GROWTH OF LINEAR RECURRENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-34
-
- Article
- Export citation
Metallic mean Wang tiles II: the dynamics of an aperiodic computer chip
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 September 2025, e155
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An explicit economical additive basis
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 12 September 2025, pp. 815-820
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RUNS IN PAPERFOLDING SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pointwise convergence of bilinear polynomial averages over the primes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 01 September 2025, pp. 3760-3799
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISTAL EXPANSIONS OF PRESBURGER ARITHMETIC BY A SPARSE PREDICATE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 28 August 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Metallic mean Wang tiles I: self-similarity, aperiodicity and minimality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 August 2025, e133
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Infinitely repeated partitions of Liouville numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 06 August 2025, pp. 1-8
-
- Article
- Export citation
DIMENSIONS OF SETS AVOIDING APPROXIMATE NONTRIVIAL ZEROS OF LINEAR PATTERNS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-12
-
- Article
- Export citation
ON ESWARATHASAN–LEVINE AND BOYD’S CONJECTURES FOR HARMONIC NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp estimates for Gowers norms on discrete cubes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1-27
-
- Article
- Export citation
 $B_h$-sets of real and complex numbers
$B_h$-sets of real and complex numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1-5
-
- Article
- Export citation
MONOTONIC COLLATZ SUBSEQUENCES WITH TERMS CONGRUENT MODULO A FIXED POWER OF TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 16 May 2025, pp. 418-429
- Print publication:
- December 2025
-
- Article
- Export citation
Uniform sets with few progressions via colourings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 15 May 2025, pp. 79-103
- Print publication:
- July 2025
-
- Article
- Export citation