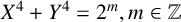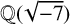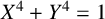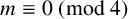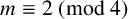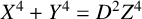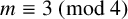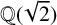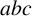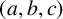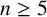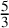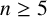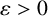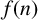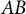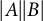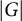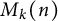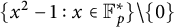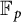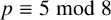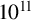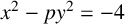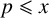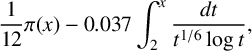Refine listing
Actions for selected content:
218 results in 11Dxx
NOTES ON GENERALISED INTEGRAL POLYNOMIAL PELL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 09 December 2025, pp. 1-13
-
- Article
- Export citation
ON THE LARGEST PRIME DIVISOR OF n! + 1
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUANTITATIVE GROWTH OF LINEAR RECURRENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-34
-
- Article
- Export citation
Improvements on dimension growth results and effective Hilbert’s irreducibility theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 September 2025, e153
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE GENERALISED RAMANUJAN–NAGELL EQUATION
 $x^2=2^m+p^n$
$x^2=2^m+p^n$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-14
-
- Article
- Export citation
Integer solutions of the generalized polynomial Pell equations and their finiteness: The quadratic case
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1-12
-
- Article
- Export citation
THE FERMAT QUARTIC X4 + Y4 = 2m IN QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number of solutions to a special type of unit equations in two unknowns, III
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 07 August 2025, pp. 737-784
- Print publication:
- November 2025
-
- Article
- Export citation
IMPROVED LOWER BOUNDS FOR STRONG n-CONJECTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 02 June 2025, pp. 61-81
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SQUARE-FULL VALUES OF QUADRATIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 16 May 2025, pp. 1-15
-
- Article
- Export citation
Multiplicative dependence in linear recurrence sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 1278-1288
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMBINATORIAL PROOFS FOR TWO-COLOUR PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-5
-
- Article
- Export citation
BINARY AND TERNARY CONGRUENCES INVOLVING INTERVALS AND SETS MODULO A PRIME
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 237-247
- Print publication:
- October 2025
-
- Article
- Export citation
Hilbert’s 10th problem via Mordell curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 939-949
- Print publication:
- September 2025
-
- Article
- Export citation
POLYNOMIALS REPRESENTED BY NORM FORMS VIA THE BETA SIEVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 25 February 2025, pp. 1463-1519
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiplicative structure of shifted multiplicative subgroups and its applications to Diophantine tuples
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 February 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXISTENCE OF K-MULTIMAGIC SQUARES AND MAGIC SQUARES OF kth POWERS WITH DISTINCT ENTRIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 441-448
- Print publication:
- December 2025
-
- Article
- Export citation
Average Analytic Ranks of Elliptic Curves over Number Fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 February 2025, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PARITY BIAS IN FUNDAMENTAL UNITS OF REAL QUADRATIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 67-70
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON PERFECT POWERS AS SUMS OR DIFFERENCES OF TWO k-GENERALISED PELL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 227-236
- Print publication:
- October 2025
-
- Article
- Export citation