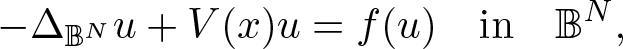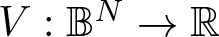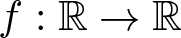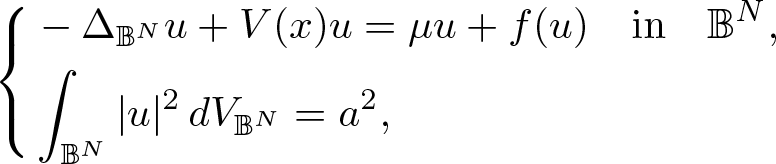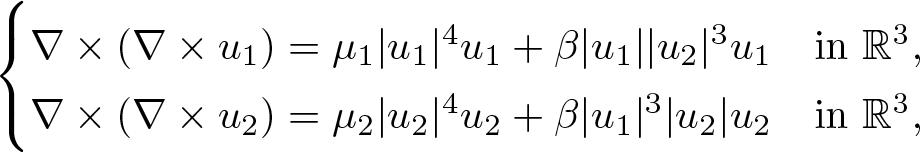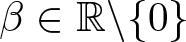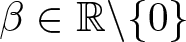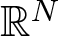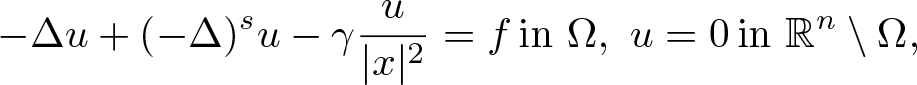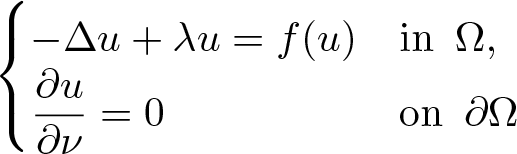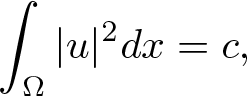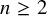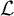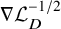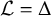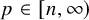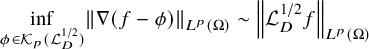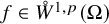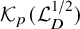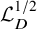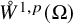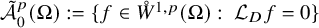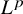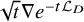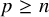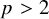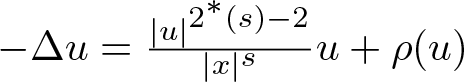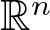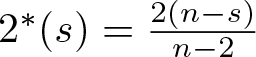Refine listing
Actions for selected content:
411 results in 35Jxx
Hardy-type inequalities for the drifting p-Laplace operator and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 August 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global existence and some qualitative properties of weak solutions for a class of pseudo-parabolic equations with a logarithmic nonlinearity in whole
 $\mathbb{R}^{N}$
$\mathbb{R}^{N}$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-44
-
- Article
- Export citation
Variational method for fractional Hamiltonian system in bounded domain
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 July 2025, pp. 1-35
-
- Article
- Export citation
Concentration and oscillation analysis of positive solutions to semilinear elliptic equations with exponential growth in a disc. II
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 July 2025, pp. 1-28
-
- Article
- Export citation
On the existence of positive solutions to some classes of elliptic problems in Hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-41
-
- Article
- Export citation
Radial and non-radial solutions for a class of (p, q)-Laplace equations involving weights
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 July 2025, pp. 1-33
-
- Article
- Export citation
Regularity results for minimizers of non-autonomous integral functionals
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 July 2025, pp. 1-28
-
- Article
- Export citation
Ground state solution for weakly coupled time-harmonic Maxwell’s equations with critical exponent
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 July 2025, pp. 1-31
-
- Article
- Export citation
Local well-posedness and blow-up in the energy space for the 2D NLS with point interaction
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 July 2025, pp. 1-20
-
- Article
- Export citation
The moving plane method and the uniqueness of high-order elliptic equation with GJMS operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 July 2025, pp. 1-45
-
- Article
- Export citation
Non-existence theorems for quasilinear elliptic equations with weights
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-33
-
- Article
- Export citation
Minimal Lagrangian submanifolds of weighted Kim–McCann metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 1223-1238
- Print publication:
- December 2025
-
- Article
- Export citation
Pattern formation with jump discontinuity in a predator–prey model with Holling-II functional response
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1160-1182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On mixed local–nonlocal problems with Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-34
-
- Article
- Export citation
The Dirichlet problem of generalized special Lagrangian type equations and curvature version
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 April 2025, pp. 1-27
-
- Article
- Export citation
Numerical solution of a PDE arising from prediction with expert advice
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solutions with prescribed mass for L2-supercritical NLS equations under Neumann boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some remarks on Riesz transforms on exterior Lipschitz domains
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 March 2025, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a perturbed critical semilinear equation with singularity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 February 2025, pp. 1-35
-
- Article
- Export citation
An elliptic operator with a nonlocal term: maximum principle, principal eigenvalue, and applications to a logistic equation with indefinite weight
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-38
-
- Article
- Export citation