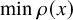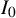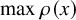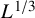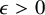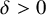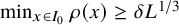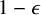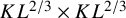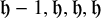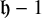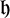Refine listing
Actions for selected content:
165 results in 82Bxx
Connectivity of a family of bilateral preference random graphs
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 18 December 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free fermionic probability theory and k-theoretic schubert calculus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 09 December 2025, e197
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inhomogeneous random graphs with infinite-mean fitness variables
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-26
-
- Article
- Export citation
Counting minimal cutsets and
 $p_c<1$
$p_c<1$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 October 2025, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness of locally stable Gibbs point processes via spatial birth–death dynamics
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 October 2025, pp. 1-36
-
- Article
- Export citation
Non-uniqueness phase in hyperbolic marked random connection models using the spherical transform
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Glauber dynamics for the hard-core model on bounded-degree
 $H$-free graphs
$H$-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 19 September 2025, pp. 803-814
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The distance on the slightly supercritical random series–parallel graph
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Colored interacting particle systems on the ring: Stationary measures from Yang–Baxter equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1855-1922
- Print publication:
- August 2025
-
- Article
- Export citation
Critical scaling profile for trees and connected subgraphs on the complete graph
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Percolation in lattice k-neighbor graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 03 June 2025, pp. 1475-1492
- Print publication:
- December 2025
-
- Article
- Export citation
Probabilistic voting models with varying speeds of Correlation decay
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 35-64
- Print publication:
- March 2025
-
- Article
- Export citation
Hypergraph independence polynomials with a zero close to the origin
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 486-490
-
- Article
- Export citation
Localization in the random XXZ quantum spin chain
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 03 January 2025, e129
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded Littlewood identity related to alternating sign matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 December 2024, e124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exponential decay for constrained-degree percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 795-807
- Print publication:
- June 2025
-
- Article
- Export citation
A note on the Winterbottom shape
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Recent kernel methods for interacting particle systems: first numerical results
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 464-489
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Expansion of the critical intensity for the random connection model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 08 November 2024, pp. 158-209
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On level line fluctuations of SOS surfaces above a wall
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e91
-
- Article
-
- You have access
- Open access
- HTML
- Export citation


























































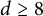










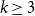
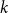
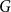
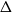
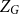
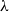
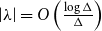
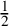






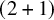
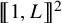 with zero boundary conditions and nonnegative heights (a floor at height
with zero boundary conditions and nonnegative heights (a floor at height 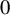
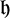
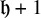
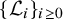
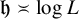
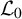
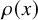
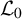
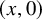
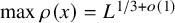
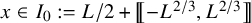 . It is believed that rescaling
. It is believed that rescaling