Refine search
Actions for selected content:
237882 results in Physics and Astronomy
PSP volume 180 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 10 February 2026, pp. f1-f2
- Print publication:
- March 2026
-
- Article
-
- You have access
- Export citation
Improvement in High-Average-Power Laser Resistance of an Optically Addressed Spatial Light Modulator Based on a New Air-Gap Structure
-
- Journal:
- High Power Laser Science and Engineering / Accepted manuscript
- Published online by Cambridge University Press:
- 10 February 2026, pp. 1-25
-
- Article
-
- You have access
- Open access
- Export citation
New sub-types and transition mechanisms within the canonical six shock interference patterns
-
- Journal:
- Journal of Fluid Mechanics / Volume 1029 / 25 February 2026
- Published online by Cambridge University Press:
- 10 February 2026, A1
-
- Article
- Export citation
Destabilisation of Alfvénic ion temperature gradient modes in the core plasma on HL-2A tokamak
-
- Journal:
- Journal of Plasma Physics / Volume 92 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 09 February 2026, E5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear stability of nanofluid boundary-layer flow over a flat plate
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 09 February 2026, A45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hybrid fluid–kinetic simulations of resistive instabilities in runaway electron beams
-
- Journal:
- Journal of Plasma Physics / Volume 92 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 09 February 2026, E3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tsunami and induced magnetic anomalies generated by slender fault
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 09 February 2026, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Self-regulating non-equilibrium in a slender body’s turbulent wake
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 09 February 2026, A49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Viscosity contrast destabilises radial Rayleigh–Taylor flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 09 February 2026, R2
-
- Article
- Export citation
Investigation on the cavitation characteristics induced by high-intensity focused ultrasonic waves in a near-wall region
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 09 February 2026, A48
-
- Article
- Export citation
Experimental measurement of the Prandtl–Meyer function in non-ideal supersonic flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 09 February 2026, A41
-
- Article
- Export citation
The SAMI Galaxy Survey: Quenching of Star Formation in Clusters III. Ram-Pressure-Affected Galaxy Populations
-
- Journal:
- Publications of the Astronomical Society of Australia / Accepted manuscript
- Published online by Cambridge University Press:
- 09 February 2026, pp. 1-26
-
- Article
-
- You have access
- Open access
- Export citation
Population synthesis of double white dwarfs: evolutionary effects on system properties
-
- Journal:
- Publications of the Astronomical Society of Australia / Accepted manuscript
- Published online by Cambridge University Press:
- 09 February 2026, pp. 1-10
-
- Article
-
- You have access
- Open access
- Export citation
Direct numerical simulation of the effects of a smooth surface hump on transition in swept-wing boundary layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 09 February 2026, A47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analytic model for neutral penetration and plasma fueling
-
- Journal:
- Journal of Plasma Physics / Volume 92 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 09 February 2026, E4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New techniques to investigate the AGN-SF connection with integral field spectroscopy
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 43 / 2026
- Published online by Cambridge University Press:
- 09 February 2026, e023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Many-Body Green's Functions for Time-Dependent Problems
-
- Published online:
- 06 February 2026
- Print publication:
- 05 March 2026
Direct generation of high-power femtosecond Laguerre-Gaussian and Bessel vortex beams in a thin-disk laser oscillator
-
- Journal:
- High Power Laser Science and Engineering / Accepted manuscript
- Published online by Cambridge University Press:
- 06 February 2026, pp. 1-18
-
- Article
-
- You have access
- Open access
- Export citation
On the generation of corner flow circulation at highly rarefied conditions
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 06 February 2026, A44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Undulatory hydrodynamics of tapered elastic plates in viscous fluid
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 06 February 2026, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation



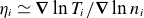
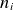
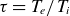
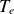
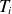




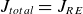
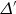








 , with σ
, with σ












