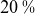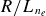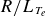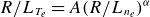Refine search
Actions for selected content:
237882 results in Physics and Astronomy
Lattice Boltzmann modelling of droplet impact and splashing at high Reynolds and Weber numbers
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 03 February 2026, A20
-
- Article
- Export citation
Magnetic steering of chiral nanobots subject to thermal noise
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 03 February 2026, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hydraulic resistance of channels obstructed by a dense array of elastic fibres
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 03 February 2026, A21
-
- Article
- Export citation
Power-law scaling of mixing in recirculation zones: non-reacting versus reacting flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 03 February 2026, A23
-
- Article
- Export citation
On the ventilation of surface-piercing hydrofoils under steady-state conditions
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 03 February 2026, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vortex dynamics of a forced globally unstable jet: breaking and preserving axisymmetry
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 03 February 2026, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Quantum Cosmology
- An Introduction
-
- Published online:
- 02 February 2026
- Print publication:
- 19 February 2026
A passive cell body plays an active role in microalgal swimming via non-reciprocal interactions
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 02 February 2026, A16
-
- Article
- Export citation
A composite mean temperature transformation for compressible turbulent boundary layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 02 February 2026, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear stability studies for a quasi-axisymmetric equilibrium including plasma flow, drift and viscosity effects
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 02 February 2026, E157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Probing the Consistency of Quantum Field Theory I
- From Nonconvergence to Haag's Theorem (1949–1954)
-
- Published online:
- 30 January 2026
- Print publication:
- 26 February 2026
-
- Element
-
- You have access
- Open access
- HTML
- Export citation
Unified scaling laws in porous-medium vertical natural convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 30 January 2026, A17
-
- Article
- Export citation
A quasi-isodynamic stellarator configuration towards a fusion power plant
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 30 January 2026, E153
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pattern selection between two-dimensional Rayleigh–Bénard convection and electroconvection near electrochemical surfaces
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 30 January 2026, A10
-
- Article
- Export citation
Parameter optimisation design of helicon wave plasma source in High Magnetic field Helicon eXperiment
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 30 January 2026, E156
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Note on a controlled interconversion between two minimal surfaces
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 30 January 2026, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Microstreaming induced by a micro-cantilever vibrating elliptically in a viscous fluid
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 30 January 2026, A11
-
- Article
-
- You have access
- HTML
- Export citation
FLM volume 1027 Cover and Front matter
-
- Journal:
- Journal of Fluid Mechanics / Volume 1027 / 25 January 2026
- Published online by Cambridge University Press:
- 30 January 2026, p. f1
-
- Article
-
- You have access
- Export citation
Laser pulse focusing and energetic electron generation by magnetised plasma lens
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 30 January 2026, E154
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reconstructions of electron-temperature profiles from EUROfusion pedestal database using turbulence models and machine learning
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 30 January 2026, E155
-
- Article
-
- You have access
- Open access
- HTML
- Export citation