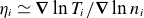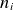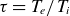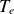Refine search
Actions for selected content:
237874 results in Physics and Astronomy
Over 30 W single-mode kilohertz-linewidth single-frequency all-fiber laser at 910 nm
-
- Journal:
- High Power Laser Science and Engineering / Accepted manuscript
- Published online by Cambridge University Press:
- 12 February 2026, pp. 1-21
-
- Article
-
- You have access
- Open access
- Export citation
Steady advection–diffusion in multiply connected potential flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 1029 / 25 February 2026
- Published online by Cambridge University Press:
- 12 February 2026, A10
-
- Article
- Export citation
Transformations of velocity and temperature for compressible turbulent boundary layers from subsonic to hypersonic regimes
-
- Journal:
- Journal of Fluid Mechanics / Volume 1029 / 25 February 2026
- Published online by Cambridge University Press:
- 12 February 2026, A12
-
- Article
- Export citation
Anisotropy of emergent large-scale dynamics in forced stratified shear flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 1029 / 25 February 2026
- Published online by Cambridge University Press:
- 12 February 2026, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the load-shifting phenomenon of accelerating reconfigurable circular plates
-
- Journal:
- Journal of Fluid Mechanics / Volume 1029 / 25 February 2026
- Published online by Cambridge University Press:
- 12 February 2026, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turbulence-induced anti-Stokes flow: experiments and theory
-
- Journal:
- Journal of Fluid Mechanics / Volume 1029 / 25 February 2026
- Published online by Cambridge University Press:
- 12 February 2026, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turbulent flame–wall interaction: dynamics of flame thickness and combustion regime
-
- Journal:
- Journal of Fluid Mechanics / Volume 1029 / 25 February 2026
- Published online by Cambridge University Press:
- 11 February 2026, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Preferential concentration and flow field modification in bubble-laden vertical turbulent channel flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1029 / 25 February 2026
- Published online by Cambridge University Press:
- 10 February 2026, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-dimensional dissipation at strong unsteady transitions in isotropic turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 10 February 2026, A46
-
- Article
- Export citation
Broadband laser absorption study based on radiochromic film combined with fiber-optic probes at the low-coherence Kunwu laser facility
-
- Journal:
- High Power Laser Science and Engineering / Accepted manuscript
- Published online by Cambridge University Press:
- 10 February 2026, pp. 1-25
-
- Article
-
- You have access
- Open access
- Export citation
PSP volume 180 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 10 February 2026, pp. b1-b2
- Print publication:
- March 2026
-
- Article
-
- You have access
- Export citation
Achieving optimal locomotion using self-generated waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 1029 / 25 February 2026
- Published online by Cambridge University Press:
- 10 February 2026, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PSP volume 180 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 10 February 2026, pp. f1-f2
- Print publication:
- March 2026
-
- Article
-
- You have access
- Export citation
Improvement in High-Average-Power Laser Resistance of an Optically Addressed Spatial Light Modulator Based on a New Air-Gap Structure
-
- Journal:
- High Power Laser Science and Engineering / Accepted manuscript
- Published online by Cambridge University Press:
- 10 February 2026, pp. 1-25
-
- Article
-
- You have access
- Open access
- Export citation
New sub-types and transition mechanisms within the canonical six shock interference patterns
-
- Journal:
- Journal of Fluid Mechanics / Volume 1029 / 25 February 2026
- Published online by Cambridge University Press:
- 10 February 2026, A1
-
- Article
- Export citation
Destabilisation of Alfvénic ion temperature gradient modes in the core plasma on HL-2A tokamak
-
- Journal:
- Journal of Plasma Physics / Volume 92 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 09 February 2026, E5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear stability of nanofluid boundary-layer flow over a flat plate
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 09 February 2026, A45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hybrid fluid–kinetic simulations of resistive instabilities in runaway electron beams
-
- Journal:
- Journal of Plasma Physics / Volume 92 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 09 February 2026, E3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tsunami and induced magnetic anomalies generated by slender fault
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 09 February 2026, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Self-regulating non-equilibrium in a slender body’s turbulent wake
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 09 February 2026, A49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation