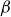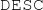Refine search
Actions for selected content:
237875 results in Physics and Astronomy
Star formation outside galaxies undergoing gravitational and hydrodynamic interactions: Dust attenuation and the star formation rate
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 43 / 2026
- Published online by Cambridge University Press:
- 29 January 2026, e019
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effect of initial spanwise perturbations on the dynamics and mixing of planar gravity currents
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 29 January 2026, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Planar intrusions from a source in quiescent and flowing ambients
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 26 January 2026, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Omnigenous umbilic stellarators
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 26 January 2026, E151
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
High-Rayleigh-number asymptotic classical scaling in three-dimensional steady natural convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 26 January 2026, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turbulent diffusion–cascade interaction
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 26 January 2026, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Neural network reconstruction of the DIII-D tokamak plasma boundary using a reduced set of diagnostics
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 26 January 2026, E152
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Separation bubble shaped control bumps for turbulent oblique shock wave–boundary-layer interactions
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 26 January 2026, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lidar observations of turbulence for tall offshore wind turbines
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 26 January 2026, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamic stall of a hydrofoil with tubercles in surface gravity waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 26 January 2026, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Setting a polyphasic approach to study Antarctic cryptoendolithic communities as a toolkit for astrobiology
-
- Journal:
- International Journal of Astrobiology / Volume 25 / 2026
- Published online by Cambridge University Press:
- 26 January 2026, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pressure drop in engineered (TPMS-based) porous media
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 26 January 2026, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the applicability of the actuator line method for unsteady aerodynamics
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 26 January 2026, A7
-
- Article
- Export citation
A way toward sub-exawatt laser: full-aperture two-grating slanted-groove compressor
-
- Journal:
- High Power Laser Science and Engineering / Accepted manuscript
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-34
-
- Article
-
- You have access
- Open access
- Export citation
Extending near-axis equilibria in
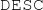 $\mathtt {DESC}$
$\mathtt {DESC}$
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 26 January 2026, E149
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Viscoelastic effects on turbulent drag reduction via a non-Newtonian lubricating layer
-
- Journal:
- Journal of Fluid Mechanics / Volume 1028 / 10 February 2026
- Published online by Cambridge University Press:
- 26 January 2026, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The effect of plasmoid drifts on the pellet rocket effect in magnetic confinement fusion plasmas
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 26 January 2026, E150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FLM volume 1026 Cover and Front matter
-
- Journal:
- Journal of Fluid Mechanics / Volume 1026 / 10 January 2026
- Published online by Cambridge University Press:
- 23 January 2026, p. f1
-
- Article
-
- You have access
- Export citation
Drag on a hollow sphere can increase with porosity
-
- Journal:
- Journal of Fluid Mechanics / Volume 1027 / 25 January 2026
- Published online by Cambridge University Press:
- 23 January 2026, A44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Curvature-based analysis of complex morphologies at early stages of atomising spray
-
- Journal:
- Journal of Fluid Mechanics / Volume 1027 / 25 January 2026
- Published online by Cambridge University Press:
- 23 January 2026, A43
-
- Article
- Export citation