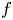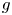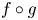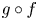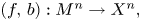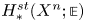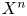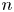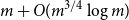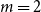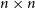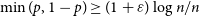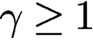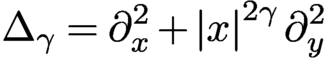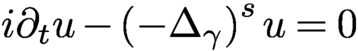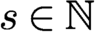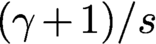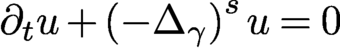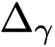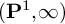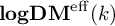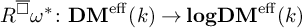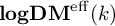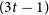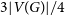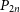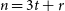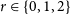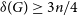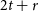Refine search
Actions for selected content:
25847 results in Abstract analysis
13 - Continuity and a.e. Continuity
-
- Book:
- Counterexamples in Measure and Integration
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 247-260
-
- Chapter
- Export citation
References
-
- Book:
- Counterexamples in Measure and Integration
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 385-393
-
- Chapter
- Export citation
1 - A Panorama of Lebesgue Integration
-
- Book:
- Counterexamples in Measure and Integration
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 1-35
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Counterexamples in Measure and Integration
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp i-iv
-
- Chapter
- Export citation
19 - Convergence of Measures
-
- Book:
- Counterexamples in Measure and Integration
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 370-384
-
- Chapter
- Export citation
9 - Inner and Outer Measure
-
- Book:
- Counterexamples in Measure and Integration
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 182-201
-
- Chapter
- Export citation
15 - Measurability on Product Spaces
-
- Book:
- Counterexamples in Measure and Integration
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 280-294
-
- Chapter
- Export citation
17 - Radon–Nikodým and Related Results
-
- Book:
- Counterexamples in Measure and Integration
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 317-329
-
- Chapter
- Export citation
Wave propagation in a diffusive SAIV epidemic model with time delays
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 16 June 2021, pp. 674-700
-
- Article
- Export citation
Parrondo's paradox for homoeomorphisms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 16 June 2021, pp. 817-825
- Print publication:
- August 2022
-
- Article
- Export citation
Dual exponential polynomials and a problem of Ozawa
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 16 June 2021, pp. 701-719
- Print publication:
- June 2022
-
- Article
- Export citation
Cahn–Hilliard equations on an evolving surface
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 16 June 2021, pp. 937-1000
-
- Article
- Export citation
Generalized manifolds, normal invariants, and 𝕃-homology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 16 June 2021, pp. 574-589
-
- Article
- Export citation
Asymptotic propagations of a nonlocal dispersal population model with shifting habitats
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 16 June 2021, pp. 701-728
-
- Article
-
- You have access
- Export citation
Card guessing with partial feedback
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 1-20
-
- Article
- Export citation
Singularity of sparse random matrices: simple proofs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 21-28
-
- Article
- Export citation
REPRESENTATION VARIETIES OF ALGEBRAS WITH NODES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 2215-2245
- Print publication:
- November 2022
-
- Article
- Export citation
OBSERVABILITY OF BAOUENDI–GRUSHIN-TYPE EQUATIONS THROUGH RESOLVENT ESTIMATES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 14 June 2021, pp. 541-579
- Print publication:
- March 2023
-
- Article
- Export citation
CONNECTIVITY AND PURITY FOR LOGARITHMIC MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 14 June 2021, pp. 335-381
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
Monochromatic paths and cycles in 2-edge-coloured graphs with large minimum degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 14 June 2021, pp. 109-122
-
- Article
- Export citation