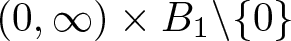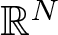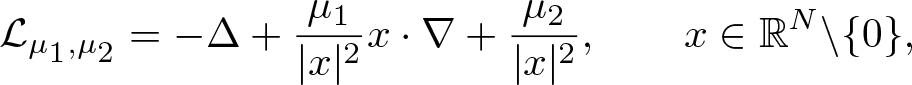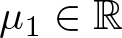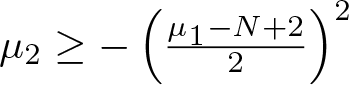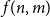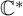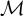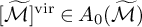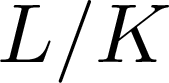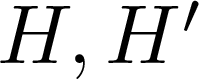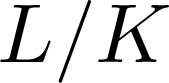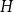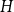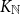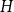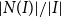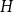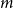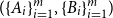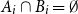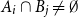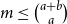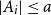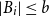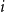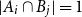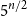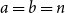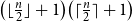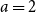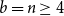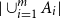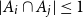Refine search
Actions for selected content:
25816 results in Abstract analysis
Spreading dynamics of a discrete Nicholson's blowflies equation with distributed delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 746-768
- Print publication:
- June 2024
-
- Article
- Export citation
Special Issue of EJAM: The Mathematics in Renewable Energy
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 08 May 2023, pp. 425-428
-
- Article
-
- You have access
- HTML
- Export citation
Extended symmetry analysis of remarkable (1+2)-dimensional Fokker–Planck equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 May 2023, pp. 1067-1098
-
- Article
- Export citation
Higher-order evolution inequalities involving convection and Hardy-Leray potential terms in a bounded domain
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 05 May 2023, pp. 366-390
-
- Article
- Export citation
Maximal chordal subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 724-741
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTRINSIC STABILIZER REDUCTION AND GENERALIZED DONALDSON–THOMAS INVARIANTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 1987-2025
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GMJ volume 65 issue 2 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 10 August 2023, pp. b1-b2
- Print publication:
- May 2023
-
- Article
-
- You have access
- Export citation
Editorial
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 26 May 2023, p. S1
- Print publication:
- May 2023
-
- Article
-
- You have access
- HTML
- Export citation
GMJ volume 65 issue S1 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. f1-f2
- Print publication:
- May 2023
-
- Article
-
- You have access
- Export citation
GMJ volume 65 issue S1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. b1-b2
- Print publication:
- May 2023
-
- Article
-
- You have access
- Export citation
GMJ volume 65 issue 2 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 10 August 2023, pp. f1-f2
- Print publication:
- May 2023
-
- Article
-
- You have access
- Export citation
A HECKE ACTION ON
 $G_1T$-MODULES
$G_1T$-MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 1125-1167
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On ρ-conjugate Hopf–Galois structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 288-304
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local regularity for nonlinear elliptic and parabolic equations with anisotropic weights
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 391-436
-
- Article
- Export citation
Gabber rigidity in hermitian K-theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 April 2023, pp. 1842-1847
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local and global existence and uniqueness of solution for abstract differential equations with state-dependent argument
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 305-345
-
- Article
- Export citation
Total mean curvature surfaces in the product space
 ${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 346-365
-
- Article
- Export citation
Ramsey upper density of infinite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 703-723
-
- Article
- Export citation
THE QUANTUM ISOMERIC SUPERCATEGORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 25 April 2023, pp. 1077-1124
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Problems and results on 1-cross-intersecting set pair systems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 691-702
-
- Article
-
- You have access
- Open access
- HTML
- Export citation