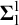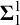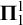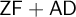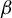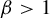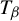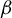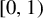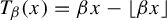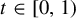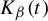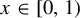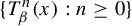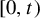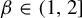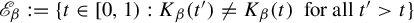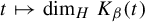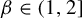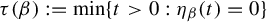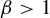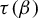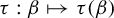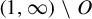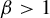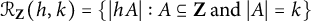Refine listing
Actions for selected content:
66 results in JMM Journal Articles Collection 2026
COHOMOLOGY ISOMORPHISM OF SYMMETRIC POWER OF COTANGENT BUNDLE OF BALL QUOTIENT AND ITS TOROIDAL COMPACTIFICATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 11 December 2025, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GOLDSTERN’S PRINCIPLE ABOUT UNIONS OF NULL SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-17
-
- Article
- Export citation
Instabilities in collapsible channel flow with a pre-tensioned elastic beam
-
- Journal:
- Journal of Fluid Mechanics / Volume 1024 / 10 December 2025
- Published online by Cambridge University Press:
- 10 December 2025, A58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PSEUDOFINITENESS AND MEASURABILITY OF THE EVERYWHERE INFINITE FOREST
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Evolution of weak, homogeneous turbulence subject to rotation and stratification: the weakly dispersive case
-
- Journal:
- Journal of Fluid Mechanics / Volume 1024 / 10 December 2025
- Published online by Cambridge University Press:
- 10 December 2025, A52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Borel-type presentation of the torus-equivariant quantum K-ring of flag manifolds of type C
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 December 2025, e198
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Monotonicity of positive solutions to equations involving fractional p-Laplacian in coercive epigraph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-13
-
- Article
- Export citation
On stability of rainbow matchings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 09 December 2025, pp. 1-14
-
- Article
- Export citation
Free fermionic probability theory and k-theoretic schubert calculus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 09 December 2025, e197
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DERANGEMENTS IN PERMUTATION GROUPS WITH TWO ORBITS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 05 December 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inequality – actuarial perspectives
-
- Journal:
- British Actuarial Journal / Volume 30 / 2025
- Published online by Cambridge University Press:
- 05 December 2025, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE HIERARCHY OF NATURAL THEORIES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Negative dependence in knockout tournaments
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-16
-
- Article
- Export citation
A nonzero-sum game with reinforcement learning under mean-variance framework
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 56 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 04 December 2025, pp. 154-180
- Print publication:
- January 2026
-
- Article
- Export citation
Uniform bounds for polynomial Carleson operators and oscillatory integrals of Radon type
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-23
-
- Article
- Export citation
Opinion dynamics with continuous age structure
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The
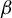 $\beta $-transformation with a hole at
$\beta $-transformation with a hole at 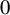 $0$: the general case
$0$: the general case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 3 / March 2026
- Published online by Cambridge University Press:
- 04 December 2025, pp. 633-659
- Print publication:
- March 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conflict-free hypergraph matchings and coverings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explicit sumset sizes in additive number theory
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-12
-
- Article
- Export citation
Operational Resilience in the UK Financial Sector Practical Guidance
-
- Journal:
- British Actuarial Journal / Volume 30 / 2025
- Published online by Cambridge University Press:
- 03 December 2025, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation