 $n$-HIGHER DERIVATIONS AND LIE
$n$-HIGHER DERIVATIONS AND LIE  $n$-HIGHER DERIVABLE MAPPINGS
$n$-HIGHER DERIVABLE MAPPINGS
 $W$-GRAPHS AND GYOJA’S
$W$-GRAPHS AND GYOJA’S  $W$-GRAPH ALGEBRA
$W$-GRAPH ALGEBRA
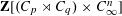 $\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{n}]$ ARE FREE
$\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{n}]$ ARE FREE
 $n$-CANONICAL MODULES OF A NOETHERIAN ALGEBRA
$n$-CANONICAL MODULES OF A NOETHERIAN ALGEBRA