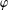 $\unicode[STIX]{x1D711}$-CONTRACTIBILITY AND
$\unicode[STIX]{x1D711}$-CONTRACTIBILITY AND 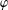 $\unicode[STIX]{x1D711}$-CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
$\unicode[STIX]{x1D711}$-CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
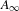 $A_{\infty }$-STRUCTURES
$A_{\infty }$-STRUCTURES
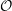 ${\mathcal{O}}$ for quantized symplectic resolutions
${\mathcal{O}}$ for quantized symplectic resolutions
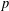 $p$
$p$