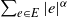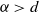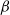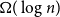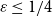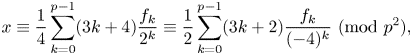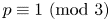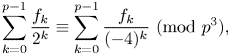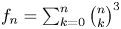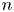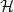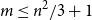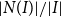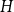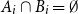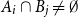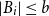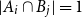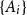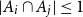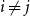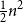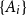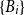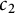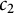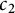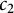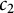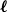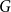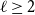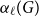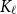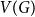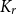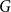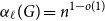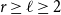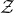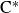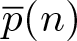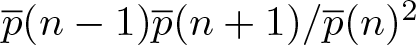Refine listing
Actions for selected content:
1717 results in 05xxx
Upper large deviations for power-weighted edge lengths in spatial random networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 34-70
- Print publication:
- March 2024
-
- Article
- Export citation
Unavoidable patterns in locally balanced colourings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 01 June 2023, pp. 796-808
-
- Article
- Export citation
The winner takes it all but one
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 26 May 2023, pp. 137-152
- Print publication:
- March 2024
-
- Article
- Export citation
Subspace coverings with multiplicities
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 18 May 2023, pp. 782-795
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A pair degree condition for Hamiltonian cycles in 3-uniform hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 17 May 2023, pp. 762-781
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On two congruence conjectures of Z.-W. Sun involving Franel numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 16 May 2023, pp. 887-905
- Print publication:
- June 2024
-
- Article
- Export citation
ON THE DIVISIBILITY OF SUMS OF q-SUPER CATALAN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 May 2023, pp. 215-224
- Print publication:
- April 2024
-
- Article
- Export citation
Universal geometric graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 742-761
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal chordal subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 724-741
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THEOREMS OF LEGENDRE TYPE FOR OVERPARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 265-275
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ramsey upper density of infinite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 703-723
-
- Article
- Export citation
Problems and results on 1-cross-intersecting set pair systems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 691-702
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A result on the
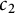 $c_2$ invariant for powers of primes
$c_2$ invariant for powers of primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1164-1178
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Clique-factors in graphs with sublinear
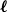 $\boldsymbol\ell$-independence number
$\boldsymbol\ell$-independence number
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 665-681
-
- Article
- Export citation
Expected number of faces in a random embedding of any graph is at most linear
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 682-690
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local limits of spatial inhomogeneous random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 April 2023, pp. 793-840
- Print publication:
- September 2023
-
- Article
- Export citation
Random amenable C*-algebras
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 12 April 2023, pp. 345-366
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Breaking of ensemble equivalence for dense random graphs under a single constraint
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1181-1200
- Print publication:
- December 2023
-
- Article
- Export citation
A generalization of Kruskal’s theorem on tensor decomposition
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 April 2023, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher order log-concavity of the overpartition function and its consequences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 164-181
-
- Article
- Export citation