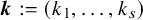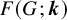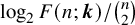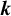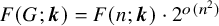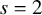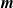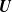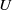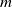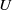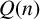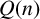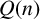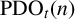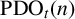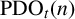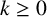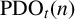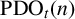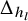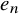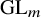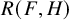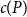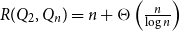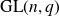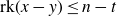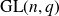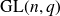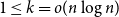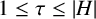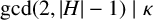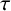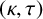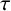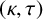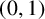Refine listing
Actions for selected content:
1717 results in 05xxx
Stability for the Erdős-Rothschild problem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Negative moments of orthogonal polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 29 March 2023, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic normality for
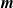 $\boldsymbol{m}$-dependent and constrained
$\boldsymbol{m}$-dependent and constrained 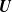 $\boldsymbol{U}$-statistics, with applications to pattern matching in random strings and permutations
$\boldsymbol{U}$-statistics, with applications to pattern matching in random strings and permutations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 March 2023, pp. 841-894
- Print publication:
- September 2023
-
- Article
- Export citation
A CONJECTURE OF MERCA ON CONGRUENCES MODULO POWERS OF 2 FOR PARTITIONS INTO DISTINCT PARTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 26-36
- Print publication:
- February 2024
-
- Article
- Export citation
On the primality of totally ordered q-factorization graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 594-637
- Print publication:
- April 2024
-
- Article
- Export citation
Concordance of spatial graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 March 2023, pp. 1091-1108
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIVISIBILITY OF THE PARTITION FUNCTION
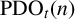 $\text {PDO}_t(n)$ BY POWERS OF
$\text {PDO}_t(n)$ BY POWERS OF 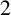 $2$ AND
$2$ AND 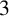 $3$
$3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 March 2023, pp. 14-25
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on weight systems which are quantum states
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 09 March 2023, pp. 1109-1121
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Degree distributions in recursive trees with fitnesses
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 March 2023, pp. 407-443
- Print publication:
- June 2023
-
- Article
- Export citation
On some hyperelliptic Hurwitz–Hodge integrals
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 271-284
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Shuffle Theorem for Paths Under Any Line
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 22 February 2023, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Proof of the Extended Delta Conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 22 February 2023, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ramsey numbers of cycles versus general graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 February 2023, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poset Ramsey numbers: large Boolean lattice versus a fixed poset
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 638-653
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersection theorems for finite general linear groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 16 February 2023, pp. 129-160
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple random walks on graphs: mixing few to cover many
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 February 2023, pp. 594-637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRAVERSING A GRAPH IN GENERAL POSITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 13 February 2023, pp. 353-365
- Print publication:
- December 2023
-
- Article
- Export citation
Random multi-hooking networks
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 13 February 2023, pp. 100-114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON REGULAR SETS IN CAYLEY GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 1-5
- Print publication:
- February 2024
-
- Article
- Export citation
Girth, magnitude homology and phase transition of diagonality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 221-247
- Print publication:
- February 2024
-
- Article
- Export citation