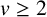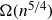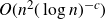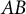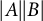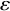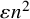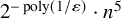Refine listing
Actions for selected content:
331 results in 11Bxx
Metallic mean Wang tiles I: self-similarity, aperiodicity and minimality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 August 2025, e133
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Infinitely repeated partitions of Liouville numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 06 August 2025, pp. 1-8
-
- Article
- Export citation
DIMENSIONS OF SETS AVOIDING APPROXIMATE NONTRIVIAL ZEROS OF LINEAR PATTERNS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-12
-
- Article
- Export citation
ON ESWARATHASAN–LEVINE AND BOYD’S CONJECTURES FOR HARMONIC NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp estimates for Gowers norms on discrete cubes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1-27
-
- Article
- Export citation
 $B_h$-sets of real and complex numbers
$B_h$-sets of real and complex numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1-5
-
- Article
- Export citation
MONOTONIC COLLATZ SUBSEQUENCES WITH TERMS CONGRUENT MODULO A FIXED POWER OF TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 16 May 2025, pp. 1-12
-
- Article
- Export citation
Uniform sets with few progressions via colourings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 15 May 2025, pp. 79-103
- Print publication:
- July 2025
-
- Article
- Export citation
THE WZ METHOD AND FLAWLESS WZ PAIRS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-9
-
- Article
- Export citation
Multiplicative dependence in linear recurrence sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 21 April 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semisimple random walks on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1-58
-
- Article
- Export citation
Improved bounds for skew corner-free sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 177-192
- Print publication:
- March 2025
-
- Article
- Export citation
The sum-product problem for integers with few prime factors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 26 June 2025, pp. 427-446
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A non-flag arithmetic regularity lemma and counting lemma
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 02 July 2025, pp. 635-679
- Print publication:
- March 2025
-
- Article
- Export citation
Multiplicative structure of shifted multiplicative subgroups and its applications to Diophantine tuples
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 February 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partition regularity of Pythagorean pairs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MINIMAL ADDITIVE COMPLEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 February 2025, pp. 1-8
-
- Article
- Export citation
An efficient asymmetric removal lemma and its limitations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CORRECTION TO ‘ADDITIVE AND SUBTRACTIVE BASES OF
 $ \mathbb {Z}_m$ IN AVERAGE’
$ \mathbb {Z}_m$ IN AVERAGE’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 566-567
- Print publication:
- June 2025
-
- Article
- Export citation
On the structure of non-negative integer sets which have identical representation functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 655-674
-
- Article
- Export citation