Refine listing
Actions for selected content:
300 results in 47Axx
Generalized Knill–Laflamme theorem for families of isoclinic subspaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 992-1010
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parabolic Muckenhoupt weights characterized by parabolic fractional maximal and integral operators with time lag
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 March 2025, pp. 1-54
-
- Article
- Export citation
Isometric dilation and Sarason’s commutant lifting theorem in several variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 25 February 2025, pp. 1-33
-
- Article
- Export citation
On a general matrix-valued unbalanced optimal transport problem
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1063-1095
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On commutators of square-zero Hilbert space operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-36
-
- Article
- Export citation
The algebraic numerical range as a spectral set in Banach algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORE ON RESTRICTED BOUNDARIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 334-344
- Print publication:
- October 2025
-
- Article
- Export citation
Absolute dilations of UCP self-adjoint Fourier multipliers: the nonunimodular case
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 14 February 2025, pp. 307-324
- Print publication:
- September 2025
-
- Article
- Export citation
Characterizations and models for the
 $C_{1,r}$ class and quantum annulus
$C_{1,r}$ class and quantum annulus
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 07 February 2025, pp. 818-833
- Print publication:
- September 2025
-
- Article
- Export citation
Extending surjective maps preserving the norm of symmetric Kubo-Ando means
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 777-786
- Print publication:
- September 2025
-
- Article
- Export citation
On several dynamical properties of shifts acting on directed trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-30
-
- Article
- Export citation
Beurling type invariant subspaces on Hardy and Bergman spaces of the unit ball or polydisk
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 232-245
- Print publication:
- March 2025
-
- Article
- Export citation
Nearly invariant Brangesian subspaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 318-337
- Print publication:
- March 2025
-
- Article
- Export citation
Central Limit Theorem for tensor products of free variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-33
-
- Article
- Export citation
Fredholm index of Toeplitz pairs with
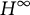 $H^{\infty }$ symbols
$H^{\infty }$ symbols
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 10 December 2024, pp. 166-176
- Print publication:
- March 2025
-
- Article
- Export citation
Survival of the flattest in the quasispecies model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 566-606
- Print publication:
- June 2025
-
- Article
- Export citation
Isometric dilations for representations of product systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerical invariants on twisted noncommutative polyballs: curvature and multiplicity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-54
-
- Article
- Export citation
Minimal isometric dilations and operator models for the polydisc
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-40
-
- Article
- Export citation
QUASI-ERGODICITY OF COMPACT STRONG FELLER SEMIGROUPS ON
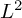 $L^2$
$L^2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 541-584
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation







 . When
. When 
 and its norm-closure
and its norm-closure  . In the infinite-dimensional setting, we characterise the intersection of
. In the infinite-dimensional setting, we characterise the intersection of  with the set of biquasitriangular operators, and we exhibit an index obstruction to belonging to
with the set of biquasitriangular operators, and we exhibit an index obstruction to belonging to  .
.






































































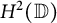

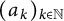
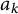
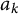
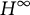

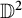

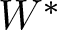
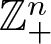
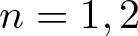
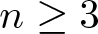
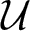
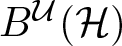

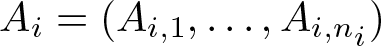
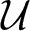
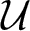
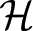
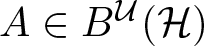
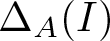
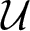


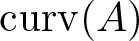


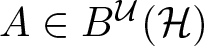
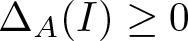

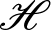
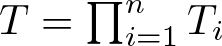


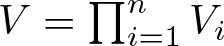


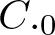
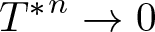
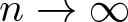

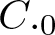
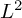








 . We discuss several applications and illustrate our results with examples. This includes a complete description of quasi-ergodicity for a large class of semigroups corresponding to non-local Schrödinger operators with confining potentials.
. We discuss several applications and illustrate our results with examples. This includes a complete description of quasi-ergodicity for a large class of semigroups corresponding to non-local Schrödinger operators with confining potentials.