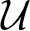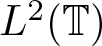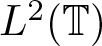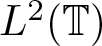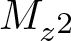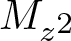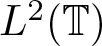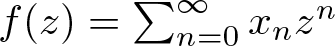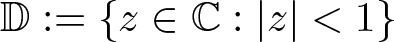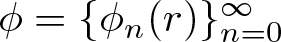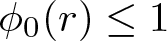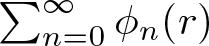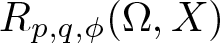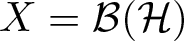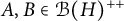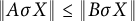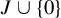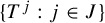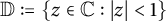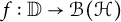Refine listing
Actions for selected content:
300 results in 47Axx
On the speed of convergence in the ergodic theorem for shift operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 04 November 2024, pp. 1919-1937
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Early warning signs for SPDEs with continuous spectrum
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 665-704
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Moment-SOS hierarchy: Applications and related topics
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 841-908
-
- Article
- Export citation
On the convexity of the quaternionic essential numerical range
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 15 May 2024, pp. 838-851
-
- Article
- Export citation
Growth of hypercyclic functions: a continuous path between
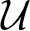 $\mathcal{U}$-frequent hypercyclicity and hypercyclicity
$\mathcal{U}$-frequent hypercyclicity and hypercyclicity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 08 May 2024, pp. 794-829
-
- Article
- Export citation
Dirichlet-type spaces of the unit bidisc and toral 2-isometries
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1271-1293
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Range inclusion and diagonalization of complex symmetric operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 04 April 2024, pp. 1222-1242
- Print publication:
- August 2025
-
- Article
- Export citation
Commutants and complex symmetry of finite Blaschke product multiplication operator in
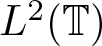 $L^2(\mathbb{T})$
$L^2(\mathbb{T})$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 261-286
-
- Article
- Export citation
Symmetric and antisymmetric tensor products for the function-theoretic operator theorist
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 December 2023, pp. 324-346
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Norms on complex matrices induced by random vectors II: extension of weakly unitarily invariant norms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 447-457
- Print publication:
- June 2024
-
- Article
- Export citation
A Lebesgue–Lusin property for linear operators of first and second order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 06 November 2023, pp. 858-868
- Print publication:
- June 2025
-
- Article
- Export citation
Bohr radius for Banach spaces on simply connected domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 113-141
-
- Article
- Export citation
Spectral mapping theorems for essential spectra and regularized functional calculi
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 12 October 2023, pp. 634-656
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tensor algebras of subproduct systems and noncommutative function theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 1587-1608
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodic solutions of four-order degenerate differential equations with finite delay in vector-valued function spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 September 2023, pp. 395-412
- Print publication:
- April 2025
-
- Article
- Export citation
Every symmetric Kubo–Ando connection has the order-determining property
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 September 2023, pp. 279-288
- Print publication:
- June 2024
-
- Article
- Export citation
Remarks on countable subadditivity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 23 August 2023, pp. 1504-1517
- Print publication:
- October 2024
-
- Article
- Export citation
Disjoint hypercyclicity, Sidon sets and weakly mixing operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1315-1329
- Print publication:
- May 2024
-
- Article
- Export citation
SPECTRAL MULTIPLIER THEOREMS FOR ABSTRACT DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 343-344
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Bohr operator on operator-valued polyanalytic functions on simply connected domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1411-1422
- Print publication:
- December 2023
-
- Article
- Export citation