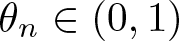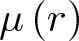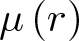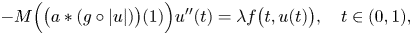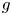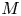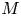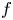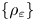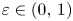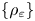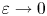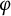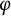Refine listing
Actions for selected content:
154 results in 26-XX
ANALYSIS OF FOURTH-ORDER DIFFERENCE APPROXIMATION SCHEMES FOR FRACTIONAL DIFFUSION EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 15 December 2025, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NEW PROOF OF THE SINGULAR CONTINUITY OF THE MINKOWSKI
 $?$-FUNCTION
$?$-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-6
-
- Article
- Export citation
The
 $\beta $-transformation with a hole at
$\beta $-transformation with a hole at  $0$: the general case
$0$: the general case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Γ-limit of weighted fractional energies
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Variation of the one-dimensional centered maximal operator on simple functions with gaps between pieces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTRAINED FRACTIONAL OPTIMIZATION PROBLEMS AND CORRESPONDING SADDLE-POINT OPTIMALITY CRITERIA
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 23 October 2025, e35
-
- Article
- Export citation
Asymptotic behavior for the sum of partial quotients in continued fraction expansions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1-13
-
- Article
- Export citation
A unified topological analysis of variable growth Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Assouad spectrum of Hölder and Sobolev graphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 01 September 2025, pp. 105-131
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semigroups of holomorphic functions; rectifiability and Lipschitz properties of the orbits
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-30
-
- Article
- Export citation
A residue theorem for rational functions on star-shaped domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 908-913
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Series expansion, higher-order monotonicity properties and inequalities for the modulus of the Grötzsch ring
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 16-43
-
- Article
- Export citation
A unified characterization of convolution coefficients in nonlocal differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
- Export citation
On some convexity questions of Handelman
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 936-939
- Print publication:
- December 2024
-
- Article
- Export citation
On the smoothness of slowly varying functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 876-891
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASYMPTOTIC BEHAVIOUR FOR PRODUCTS OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 448-459
- Print publication:
- December 2024
-
- Article
- Export citation
Sharp conditions for the validity of the Bourgain–Brezis–Mironescu formula
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-24
-
- Article
- Export citation
Uniqueness and Hyers–Ulam’s stability for a fractional nonlinear partial integro-differential equation with variable coefficients and a mixed boundary condition
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1377-1397
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theoretical study of a
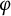 $\varphi $-Hilfer fractional differential system in Banach spaces
$\varphi $-Hilfer fractional differential system in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 27 February 2024, pp. 742-759
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A UNIFIED APPROACH TO HINDMAN, RAMSEY, AND VAN DER WAERDEN SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-53
-
- Article
- Export citation