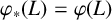Refine listing
Actions for selected content:
543 results in 22xxx
Small doubling for discrete subsets of non-commutative groups and a theorem of Lagarias
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 17 December 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DETECTING IDEALS IN REDUCED CROSSED PRODUCT C*-ALGEBRAS OF TOPOLOGICAL DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 16 December 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolic geometry and real moduli of five points on the line
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE OPEN MAPPINGS OF LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-8
-
- Article
- Export citation
DEFORMATION OF FELL BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 31 October 2025, pp. 347-381
- Print publication:
- December 2025
-
- Article
- Export citation
The dual pair
 $\mathrm {Aut}(C)\times F_{4}$ (p-adic case)
$\mathrm {Aut}(C)\times F_{4}$ (p-adic case)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 October 2025, e174
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DENOMINATORS IN LUSZTIG’S ASYMPTOTIC HECKE ALGEBRA VIA THE PLANCHEREL FORMULA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterisation of Locally Compact Abelian Groups Having Spectral Synthesis
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e145
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On homological properties of the Schlichting completion
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROPERTY (T) AND STRONG 1-BOUNDEDNESS FOR VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-34
-
- Article
- Export citation
Quasi-invariant lifts of completely positive maps for groupoid actions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 19 August 2025, pp. 1-29
-
- Article
- Export citation
CHARACTERISATION OF DISTAL ACTIONS OF AUTOMORPHISMS ON THE SPACE OF ONE-PARAMETER SUBGROUPS OF LIE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 15 August 2025, pp. 152-175
- Print publication:
- October 2025
-
- Article
- Export citation
Density and unitarity of the Burau representation from a non-semisimple TQFT
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-29
-
- Article
- Export citation
EISENSTEIN COHOMOLOGY FOR ORTHOGONAL GROUPS AND THE SPECIAL VALUES OF L-FUNCTIONS FOR
 $\mathrm {GL}_1 \times \mathrm {O}(2n)$
$\mathrm {GL}_1 \times \mathrm {O}(2n)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 2463-2522
- Print publication:
- November 2025
-
- Article
- Export citation
ÉTALE STRUCTURES AND THE JOYAL–TIERNEY REPRESENTATION THEOREM IN COUNTABLE MODEL THEORY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 July 2025, pp. 1-52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quaternionic Satake equivalence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1615-1663
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tilting sheaves for real groups and Koszul duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1698-1777
- Print publication:
- July 2025
-
- Article
- Export citation
On non-tameness of the Ellis semigroup
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 3419-3429
- Print publication:
- November 2025
-
- Article
- Export citation
Moments, Exponential Sums, and Monodromy Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 June 2025, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Locally compact modules over abelian groups and compactly generated metabelian groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1250-1283
- Print publication:
- June 2025
-
- Article
- Export citation









 -groupoid algebras to the general twisted setting.
-groupoid algebras to the general twisted setting.