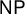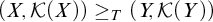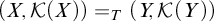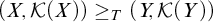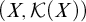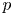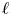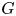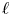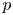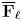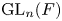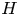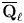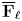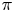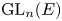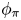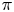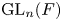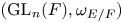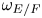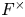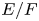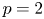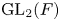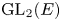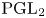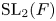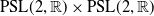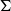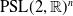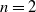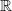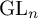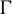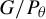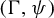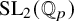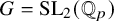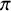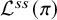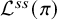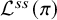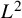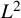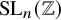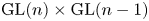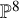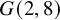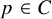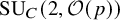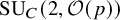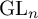Refine listing
Actions for selected content:
543 results in 22xxx
All Kronecker coefficients are reduced Kronecker coefficients
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 November 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EXAMPLE OF THE JANTZEN FILTRATION OF A D-MODULE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 265-296
- Print publication:
- June 2025
-
- Article
- Export citation
The weak Ramsey property and extreme amenability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some mod p representations of quaternion algebra over ℚp
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 03 December 2024, pp. 2585-2655
- Print publication:
- November 2024
-
- Article
- Export citation
THE SHAPE OF COMPACT COVERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-15
-
- Article
- Export citation
Whittaker coefficients of geometric Eisenstein series
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 16 October 2024, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE WEYL TRANSFORM OF A SMOOTH MEASURE ON A REAL-ANALYTIC SUBMANIFOLD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 184-193
- Print publication:
- August 2025
-
- Article
- Export citation
Modulo ℓ distinction problems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 30 September 2024, pp. 2285-2321
- Print publication:
- October 2024
-
- Article
- Export citation
Hyperbolic actions of higher rank lattices come from rank-one factors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 961-988
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weyl chamber length compactification of the
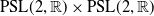 $\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
$\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 11-33
- Print publication:
- January 2025
-
- Article
- Export citation
PARITY OF CONJUGATE SELF-DUAL REPRESENTATIONS OF INNER FORMS OF
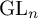 $\operatorname { {GL}}_n$ OVER p-ADIC FIELDS
$\operatorname { {GL}}_n$ OVER p-ADIC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 September 2024, pp. 249-271
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-concentration property of Patterson–Sullivan measures for Anosov subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 884-893
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability in the category of smooth mod-p representations of
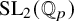 ${\mathrm {SL}}_2(\mathbb {Q}_p)$
${\mathrm {SL}}_2(\mathbb {Q}_p)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local parameters of supercuspidal representations
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the local
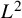 $L^2$-Bound of the Eisenstein series
$L^2$-Bound of the Eisenstein series
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 September 2024, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Period relations for Rankin–Selberg convolutions for
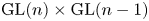 ${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1871-1915
- Print publication:
- August 2024
-
- Article
- Export citation
Connes fusion of spinors on loop space
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1596-1650
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED GAN–GROSS–PRASAD CONJECTURE FOR CERTAIN TEMPERED L-PACKETS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 May 2024, pp. 17-39
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Coble quadric
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 May 2024, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARCHIMEDEAN NEWFORM THEORY FOR
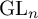 $\operatorname {\mathrm {GL}}_n$
$\operatorname {\mathrm {GL}}_n$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 May 2024, pp. 41-116
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation