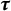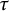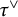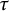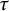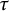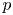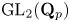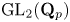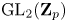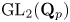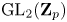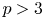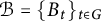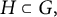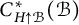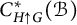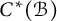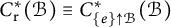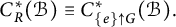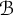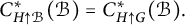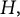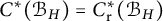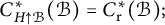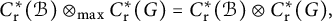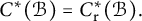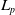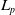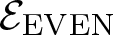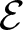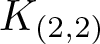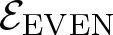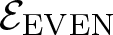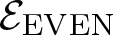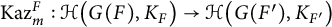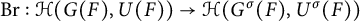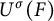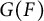Refine listing
Actions for selected content:
540 results in 22xxx
TWISTED RUELLE ZETA FUNCTION ON HYPERBOLIC MANIFOLDS AND COMPLEX-VALUED ANALYTIC TORSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 813-845
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Closed approximate subgroups: compactness, amenability and approximate lattices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
$C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 366-379
- Print publication:
- October 2025
-
- Article
- Export citation
Presentation of an Iwasawa algebra: The pro-p Iwahori of simple, simply connected, split groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 377-394
- Print publication:
- June 2025
-
- Article
- Export citation
On infinitesimal
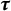 $\boldsymbol { \tau }$-isospectrality of locally symmetric spaces
$\boldsymbol { \tau }$-isospectrality of locally symmetric spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 246-261
- Print publication:
- March 2025
-
- Article
- Export citation
Restriction of p-adic representations of GL2(Qp) to parahoric subgroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 74-119
- Print publication:
- January 2025
-
- Article
- Export citation
A nonabelian Fourier transform for tempered unipotent representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 13-73
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Szemerédi type theorem for sets of positive density in approximate lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2023-2053
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear repetitivity beyond abelian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1947-1997
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cross-sectional C*-algebras associated with subgroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 December 2024, pp. 1-26
-
- Article
- Export citation
Transference of multilinear Fourier and Schur multipliers acting on noncommutative
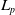 $L_p$-spaces for non-unimodular groups
$L_p$-spaces for non-unimodular groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 197-223
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generic properties of topological groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Riemannian and Ricci curvatures of homogeneous Finsler manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 73-90
- Print publication:
- March 2025
-
- Article
- Export citation
The planar 3-colorable subgroup ε of Thompson’s group F and its even part
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 173-197
-
- Article
- Export citation
Compatibility of Kazhdan and Brauer homomorphism
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 19-43
- Print publication:
- March 2025
-
- Article
- Export citation
Entropy of group actions beyond uniform lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1461-1502
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CYT and SKT manifolds with parallel Bismut torsion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
All Kronecker coefficients are reduced Kronecker coefficients
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 November 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EXAMPLE OF THE JANTZEN FILTRATION OF A D-MODULE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 265-296
- Print publication:
- June 2025
-
- Article
- Export citation
The weak Ramsey property and extreme amenability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation