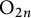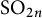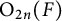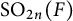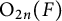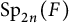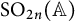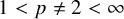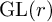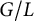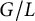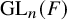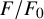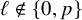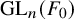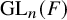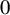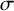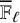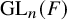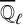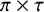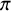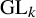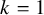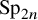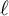Refine listing
Actions for selected content:
540 results in 22xxx
Newell–Littlewood numbers III: Eigencones and GIT-semigroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1054-1074
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-polynomial representations of double affine Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 April 2025, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The local converse theorem for quasi-split
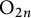 $\mathrm {O}_{2n}$ and
$\mathrm {O}_{2n}$ and 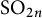 $\mathrm {SO}_{2n}$
$\mathrm {SO}_{2n}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-38
-
- Article
- Export citation
Invariant divisors and equivariant line bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Every locally compact group is the outer automorphism group of a II1 factor
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 March 2025, pp. 1-12
-
- Article
- Export citation
The local geometry of idempotent Schur multipliers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SIMPLE TYPE THEORY FOR METAPLECTIC COVERS OF
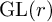 $\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
$\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1263-1335
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arthur packets for pure real forms of symplectic and special orthogonal groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1-22
-
- Article
- Export citation
Reversibility and transitivity of semigroup actions on homogeneous spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-20
-
- Article
- Export citation
Cuspidal
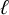 ${\ell }$-modular representations of
${\ell }$-modular representations of 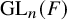 $\operatorname {GL}_n({ F})$ distinguished by a Galois involution
$\operatorname {GL}_n({ F})$ distinguished by a Galois involution
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 February 2025, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ample Groupoids, Topological Full groups, Algebraic K-theory Spectra and Infinite Loop Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hardy spaces and Riesz transforms on a Lie group of exponential growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 731-762
-
- Article
- Export citation
An Iwahori theoretic mod
 $p$ local Langlands correspondence
$p$ local Langlands correspondence
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 805-817
- Print publication:
- September 2025
-
- Article
- Export citation
Doubling constructions and tensor product L-functions: coverings of the symplectic group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RANK 2
 $\ell $-ADIC LOCAL SYSTEMS AND HIGGS BUNDLES OVER A CURVE
$\ell $-ADIC LOCAL SYSTEMS AND HIGGS BUNDLES OVER A CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 891-960
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDED CONJUGACY CLASSES AND CONJUGACY CLASSES SUPPORTING INVARIANT MEASURES AND AUTOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 06 February 2025, pp. 509-514
- Print publication:
- December 2025
-
- Article
- Export citation
The imprimitivity Fell bundle
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-44
-
- Article
- Export citation
ON EQUIVALENCE RELATIONS INDUCED BY POLISH GROUPS ADMITTING COMPATIBLE TWO-SIDED INVARIANT METRICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-38
-
- Article
- Export citation
Local newforms for generic representations of unramified even unitary groups I: Even conductor case
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 February 2025, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rich representations and superrigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 2249-2272
- Print publication:
- August 2025
-
- Article
- Export citation