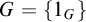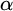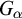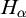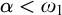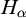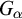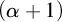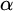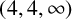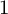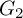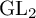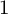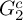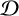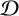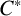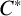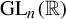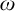Refine listing
Actions for selected content:
540 results in 22xxx
Macroscopic limit of a Fokker-Planck model of swarming rigid bodies
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 April 2024, pp. 349-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DISTINCTION OF IWAHORI-SPHERICAL DISCRETE SERIES REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-15
- Print publication:
- January 2025
-
- Article
- Export citation
SPHERICAL REPRESENTATIONS FOR
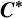 $\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
$\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 239-272
- Print publication:
- October 2024
-
- Article
- Export citation
A NONCOMMUTATIVE ANALOGUE OF CLAUSEN’S VIEW ON THE IDÈLE CLASS GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 2777-2824
- Print publication:
- November 2024
-
- Article
- Export citation
Approximate homomorphisms and sofic approximations of orbit equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 3455-3480
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structural, point-free, non-Hausdorff topological realization of Borel groupoid actions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 March 2024, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrepancy of rational points in simple algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 836-877
- Print publication:
- April 2024
-
- Article
- Export citation
The sup-norm problem beyond the newform
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 12 March 2024, pp. 517-545
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RADU GROUPS ACTING ON TREES ARE CCR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 149-186
- Print publication:
- October 2024
-
- Article
- Export citation
A NOTE ON PROJECTIONS IN ÉTALE GROUPOID ALGEBRAS AND DIAGONAL-PRESERVING HOMOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 508-513
- Print publication:
- December 2024
-
- Article
- Export citation
DIOPHANTINE TRANSFERENCE PRINCIPLE OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 216-233
- Print publication:
- October 2024
-
- Article
- Export citation
On denseness of horospheres in higher rank homogeneous spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 February 2024, pp. 3272-3289
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral equivariant cohomology of affine Grassmannians
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 727-741
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A HIERARCHY ON NON-ARCHIMEDEAN POLISH GROUPS ADMITTING A COMPATIBLE COMPLETE LEFT-INVARIANT METRIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1-19
-
- Article
- Export citation
ON THE LIMIT SET OF A COMPLEX HYPERBOLIC TRIANGLE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 02 February 2024, pp. 338-345
- Print publication:
- October 2024
-
- Article
- Export citation
COUNTING DISCRETE, LEVEL-
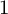 $1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON
$1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON 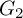 $G_2$
$G_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 2127-2157
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITELY PRESENTED INVERSE SEMIGROUPS WITH FINITELY MANY IDEMPOTENTS IN EACH
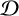 $\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
$\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 384-398
- Print publication:
- June 2024
-
- Article
- Export citation
Random and mean Lyapunov exponents for
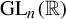 $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2063-2079
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HIGHER MOMENT FORMULAE AND LIMITING DISTRIBUTIONS OF LATTICE POINTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2081-2125
- Print publication:
- September 2024
-
- Article
- Export citation
ON THE ZARISKI TOPOLOGY ON ENDOMORPHISM MONOIDS OF OMEGA-CATEGORICAL STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 31 October 2023, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation




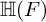
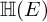
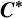
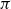
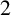
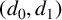
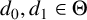







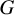
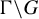
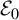
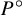
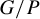
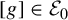
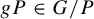
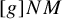
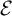
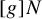
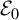
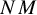
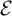
 .
.