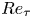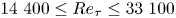Open access
Contents
JFM Papers
Sliding, vibrating and swinging droplets on an oscillating fibre
-
- Published online by Cambridge University Press:
- 19 July 2023, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characteristics of fluid–fluid displacement in model mixed-wet porous media: patterns, pressures and scalings
-
- Published online by Cambridge University Press:
- 19 July 2023, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the onset of long-wavelength three-dimensional instability in the cylinder wake
-
- Published online by Cambridge University Press:
- 18 July 2023, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An unstable mode of the stratified atmosphere under the non-traditional Coriolis acceleration
-
- Published online by Cambridge University Press:
- 18 July 2023, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A mechanistic evaluation of the local Bloch wave approximation in graded arrays of vertical barriers
-
- Published online by Cambridge University Press:
- 18 July 2023, A20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Highly singular slip length for longitudinal shear flow over a dense bubble mattress
-
- Published online by Cambridge University Press:
- 18 July 2023, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
On high-Taylor-number Taylor vortices
-
- Published online by Cambridge University Press:
- 17 July 2023, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Propulsion due to thermal streaming
-
- Published online by Cambridge University Press:
- 17 July 2023, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Formation and evolution of vortex rings with weak to moderate swirl
-
- Published online by Cambridge University Press:
- 17 July 2023, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The hunt for the Kármán ‘constant’ revisited
-
- Published online by Cambridge University Press:
- 17 July 2023, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A nematic liquid crystal with an immersed body: equilibrium, stress and paradox
-
- Published online by Cambridge University Press:
- 17 July 2023, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wind-generated waves on a water layer of finite depth
-
- Published online by Cambridge University Press:
- 17 July 2023, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Three-dimensional numerical investigation of a transversely oscillating slotted cylinder and its applications in energy harvesting
-
- Published online by Cambridge University Press:
- 13 July 2023, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Towards a finite-time singularity of the Navier–Stokes equations. Part 3. Maximal vorticity amplification
-
- Published online by Cambridge University Press:
- 12 July 2023, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Global stability analysis of elastic aircraft in edge-of-the-envelope flow
-
- Published online by Cambridge University Press:
- 12 July 2023, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Engineering of branched fluidic networks that minimise energy dissipation
-
- Published online by Cambridge University Press:
- 12 July 2023, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
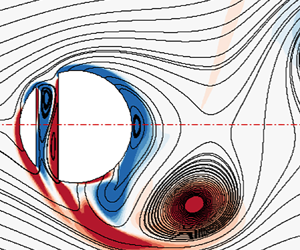
Influence of heterogeneity or shape on the locomotion of a caged squirmer
-
- Published online by Cambridge University Press:
- 12 July 2023, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
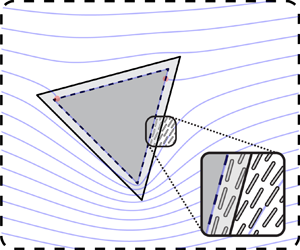
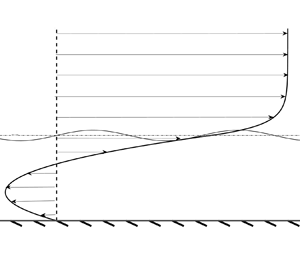
Towards decoupling the effects of permeability and roughness on turbulent boundary layers
-
- Published online by Cambridge University Press:
- 12 July 2023, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Evolution of an elastic blister in the presence of sloping topography
-
- Published online by Cambridge University Press:
- 12 July 2023, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear stability analysis of wake vortices by a spectral method using mapped Legendre functions
-
- Published online by Cambridge University Press:
- 11 July 2023, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation